Carl Friedrich Gauss

1.1. Masa Kecil dan Pendidikan

Johann Carl Friedrich Gauss lahir pada 30 April 1777 di Braunschweig, Kadipaten Brunswick-Wolfenbüttel (sekarang di negara bagian Lower Saxony, Jerman). Keluarganya memiliki status sosial yang relatif rendah. Ayahnya, Gebhard Dietrich Gauss (1744-1808), bekerja sebagai tukang daging, tukang batu, tukang kebun, dan bendahara dana santunan kematian. Gauss menggambarkan ayahnya sebagai orang yang terhormat dan dihormati, tetapi kasar dan mendominasi di rumah. Ayahnya berpengalaman dalam menulis dan berhitung, sedangkan ibu Carl Friedrich, Dorothea, hampir buta huruf. Gauss memiliki satu kakak laki-laki dari pernikahan pertama ayahnya.

Gauss adalah seorang anak ajaib dalam matematika. Sebuah anekdot terkenal menceritakan bahwa pada usia tiga tahun, ia mampu mengoreksi kesalahan perhitungan gaji tukang batu ayahnya. Kisah lain yang sering diceritakan adalah ketika ia berusia tujuh tahun di sekolah dasar, gurunya, J.G. Büttner, memberikan tugas untuk menjumlahkan semua bilangan bulat dari 1 hingga 100. Gauss dengan cepat memberikan jawaban yang benar, 5050, dengan menyadari bahwa ia dapat menjumlahkan pasangan angka dari ujung berlawanan deret (1+100=101, 2+99=101, dst.), menghasilkan 50 pasangan yang masing-masing berjumlah 101. Meskipun detail cerita ini bervariasi, intinya menunjukkan bakat luar biasa Gauss sejak dini.

Ketika guru-guru sekolah dasar menyadari kemampuan intelektualnya, mereka membawa Gauss ke perhatian Adipati Brunswick yang kemudian mengirimnya ke Collegium Carolinum setempat. Ia belajar di sana dari tahun 1792 hingga 1795, dengan Eberhard August Wilhelm von Zimmermann sebagai salah satu gurunya. Setelah itu, Adipati memberinya sumber daya untuk studi matematika, sains, dan filologi klasik di Universitas Göttingen hingga tahun 1798. Profesor matematikanya adalah Abraham Gotthelf Kästner, yang Gauss juluki "matematikawan terkemuka di antara para penyair, dan penyair terkemuka di antara para matematikawan" karena epigramnya. Astronomi diajarkan oleh Karl Felix Seyffer, dengan siapa Gauss tetap berkorespondensi setelah lulus. Ia sangat menghargai Georg Christoph Lichtenberg, guru fisika, dan Christian Gottlob Heyne, yang kuliahnya dalam klasik dihadiri Gauss dengan senang hati. Rekan-rekan mahasiswa pada masa itu antara lain Johann Friedrich Benzenberg, Farkas Bolyai, dan Heinrich Wilhelm Brandes.

Gauss kemungkinan besar adalah seorang mahasiswa otodidak dalam matematika karena ia secara mandiri menemukan kembali beberapa teorema. Ia memecahkan masalah geometris yang telah menyibukkan para matematikawan sejak Yunani Kuno ketika ia menentukan pada tahun 1796 poligon beraturan mana yang dapat dibangun dengan konstruksi kompas dan penggaris. Penemuan ini akhirnya membuat Gauss memilih matematika daripada filologi sebagai karier. Buku harian matematikanya, kumpulan catatan singkat tentang hasil-hasilnya dari tahun 1796 hingga 1814, menunjukkan bahwa banyak ide untuk karya agungnya Disquisitiones Arithmeticae (1801) berasal dari masa ini.

1.2. Cendekiawan Privat

Gauss lulus sebagai Doktor Filsafat pada tahun 1799, bukan di Göttingen, melainkan di Universitas Helmstedt atas permintaan khusus Adipati Brunswick. Johann Friedrich Pfaff menilai tesis doktoralnya, dan Gauss mendapatkan gelar in absentia tanpa ujian lisan lebih lanjut. Adipati kemudian memberinya biaya hidup sebagai cendekiawan privat di Brunswick. Gauss kemudian menolak panggilan dari Akademi Ilmu Pengetahuan Rusia di St. Petersburg dan Universitas Landshut. Adipati kemudian menjanjikannya pendirian observatorium di Brunswick pada tahun 1804. Arsitek Peter Joseph Krahe membuat desain awal, tetapi salah satu perang Napoleon membatalkan rencana tersebut: Adipati terbunuh dalam Pertempuran Jena-Auerstedt pada tahun 1806. Kadipaten dihapuskan pada tahun berikutnya, dan dukungan finansial Gauss terhenti.

Ketika Gauss menghitung orbit asteroid pada tahun-tahun pertama abad ini, ia menjalin kontak dengan komunitas astronomi Bremen dan Lilienthal, terutama Wilhelm Olbers, Karl Ludwig Harding, dan Friedrich Wilhelm Bessel, sebagai bagian dari kelompok astronom informal yang dikenal sebagai Celestial police. Salah satu tujuan mereka adalah penemuan planet-planet lebih lanjut. Mereka mengumpulkan data tentang asteroid dan komet sebagai dasar untuk penelitian Gauss tentang orbit mereka, yang kemudian ia terbitkan dalam karya astronomi agungnya Theoria motus corporum coelestium (1809).

1.3. Profesor di Göttingen

Pada November 1807, Gauss menerima panggilan ke Universitas Göttingen, yang saat itu merupakan institusi dari Kerajaan Westphalia yang baru didirikan di bawah Jérôme Bonaparte, sebagai profesor penuh dan direktur observatorium astronomi, dan mempertahankan jabatannya hingga kematiannya pada tahun 1855. Ia segera dihadapkan pada tuntutan dua ribu franc dari pemerintah Westphalia sebagai kontribusi perang, yang tidak mampu ia bayar. Baik Olbers maupun Pierre-Simon Laplace ingin membantunya dengan pembayaran tersebut, tetapi Gauss menolak bantuan mereka. Akhirnya, seseorang yang tidak dikenal dari Frankfurt, yang kemudian diketahui adalah Pangeran-primata Karl Theodor Anton Maria von Dalberg, membayar jumlah tersebut.

Gauss mengambil alih direktur observatorium berusia 60 tahun, yang didirikan pada tahun 1748 oleh Pangeran-elektor George II dari Britania Raya dan dibangun di atas menara benteng yang diubah, dengan instrumen yang dapat digunakan, tetapi sebagian sudah usang. Pembangunan observatorium baru telah disetujui oleh Pangeran-elektor George III secara prinsip sejak tahun 1802, dan pemerintah Westphalia melanjutkan perencanaan, tetapi Gauss baru dapat pindah ke tempat kerja barunya pada September 1816. Ia mendapatkan instrumen baru yang mutakhir, termasuk dua lingkaran meridian dari Repsold dan Reichenbach, dan sebuah heliometer dari Fraunhofer.

Aktivitas ilmiah Gauss, selain matematika murni, secara kasar dapat dibagi menjadi tiga periode: astronomi adalah fokus utama dalam dua dekade pertama abad ke-19, geodesi pada dekade ketiga, dan fisika, terutama magnetisme, pada dekade keempat.

Gauss tidak merahasiakan ketidaksukaannya untuk memberikan kuliah akademik. Namun, sejak awal karier akademiknya di Göttingen, ia terus memberikan kuliah hingga tahun 1854. Ia sering mengeluh tentang beban mengajar, merasa bahwa itu adalah pemborosan waktunya. Di sisi lain, ia kadang-kadang menggambarkan beberapa siswa sebagai berbakat. Sebagian besar kuliahnya membahas astronomi, geodesi, dan matematika terapan, dan hanya tiga kuliah tentang mata pelajaran matematika murni. Beberapa siswa Gauss kemudian menjadi matematikawan, fisikawan, dan astronom terkenal: Moritz Cantor, Dedekind, Dirksen, Encke, Gould, Heine, Klinkerfues, Kupffer, Listing, Möbius, Nicolai, Riemann, Ritter, Schering, Scherk, Schumacher, von Staudt, Stern, Ursin; serta geosaintis Sartorius von Waltershausen, dan Wappäus.

Gauss tidak menulis buku teks dan tidak menyukai popularisasi masalah ilmiah. Satu-satunya upayanya dalam popularisasi adalah karyanya tentang tanggal Paskah (1800/1802) dan esai Erdmagnetismus und Magnetometer tahun 1836. Gauss menerbitkan makalah dan bukunya secara eksklusif dalam bahasa Latin atau bahasa Jerman. Ia menulis Latin dalam gaya klasik tetapi menggunakan beberapa modifikasi kebiasaan yang ditetapkan oleh matematikawan kontemporer.

Dalam kuliah perdananya di Universitas Göttingen pada tahun 1808, Gauss mengklaim observasi yang andal dan hasil yang dicapai hanya dengan kalkulus yang kuat sebagai satu-satunya tugas astronomi. Di universitas, ia ditemani oleh staf pengajar lain dalam disiplin ilmunya, yang melengkapi program pendidikan; ini termasuk matematikawan Thibaut dengan kuliahnya, fisikawan Mayer, yang dikenal karena buku teksnya, penggantinya Weber sejak tahun 1831, dan di observatorium Harding, yang mengambil bagian utama kuliah dalam astronomi praktis. Ketika observatorium selesai, Gauss mengambil tempat tinggalnya di sayap barat observatorium baru dan Harding di sayap timur. Mereka pernah berteman akrab, tetapi seiring waktu mereka menjadi terasing, mungkin - seperti yang diasumsikan beberapa biografer - karena Gauss berharap Harding yang setara dengannya tidak lebih dari asisten atau pengamatnya. Gauss menggunakan lingkaran meridian baru hampir secara eksklusif, dan menjauhkannya dari Harding, kecuali untuk beberapa observasi bersama yang sangat jarang.

Martin Brendel membagi aktivitas astronomi Gauss secara kronologis menjadi tujuh periode, di mana tahun-tahun sejak 1820 dianggap sebagai "periode aktivitas astronomi yang lebih rendah". Observatorium baru yang dilengkapi dengan baik tidak bekerja seefektif yang lain; penelitian astronomi Gauss memiliki karakter perusahaan satu orang tanpa program observasi jangka panjang, dan universitas hanya menetapkan tempat untuk asisten setelah Harding meninggal pada tahun 1834.

Meskipun demikian, Gauss dua kali menolak kesempatan untuk menyelesaikan masalah dengan menerima tawaran dari Berlin pada tahun 1810 dan 1825 untuk menjadi anggota penuh Akademi Prusia tanpa beban tugas mengajar, serta dari Universitas Leipzig pada tahun 1810 dan dari Universitas Wina pada tahun 1842, mungkin karena situasi keluarga yang sulit. Gaji Gauss dinaikkan dari 1000 Reichsthaler pada tahun 1810 menjadi 2400 Reichsthaler pada tahun 1824, dan di tahun-tahun terakhirnya ia adalah salah satu profesor dengan gaji tertinggi di universitas.

Ketika Gauss dimintai bantuan oleh rekan dan temannya Friedrich Wilhelm Bessel pada tahun 1810, yang mengalami masalah di Universitas Königsberg karena kurangnya gelar akademik, Gauss memberikan doktor honoris causa untuk Bessel dari Fakultas Filsafat Göttingen pada Maret 1811. Gauss memberikan rekomendasi lain untuk gelar kehormatan bagi Sophie Germain tetapi hanya sesaat sebelum kematiannya, sehingga ia tidak pernah menerimanya. Ia juga memberikan dukungan yang berhasil kepada matematikawan Gotthold Eisenstein di Berlin.

Gauss setia kepada Wangsa Hanover. Setelah Raja William IV meninggal pada tahun 1837, Raja Hanoverian yang baru, Ernest Augustus, Raja Hanover, membatalkan konstitusi tahun 1833. Tujuh profesor, yang kemudian dikenal sebagai "Tujuh Göttingen", memprotes hal ini, di antaranya teman dan kolaboratornya Wilhelm Weber dan menantu Gauss, Heinrich Ewald. Mereka semua diberhentikan, dan tiga di antaranya diusir, tetapi Ewald dan Weber dapat tetap tinggal di Göttingen. Gauss sangat terpengaruh oleh pertengkaran ini tetapi tidak melihat kemungkinan untuk membantu mereka.

Gauss mengambil bagian dalam administrasi akademik: tiga kali ia terpilih sebagai dekan Fakultas Filsafat. Karena dipercaya dengan dana pensiun janda universitas, ia berurusan dengan ilmu aktuaria dan menulis laporan tentang strategi untuk menstabilkan tunjangan. Ia diangkat sebagai direktur Akademi Ilmu Pengetahuan Göttingen selama sembilan tahun.

1.4. Kehidupan Keluarga

Gauss menikah dengan Johanna Osthoff pada 9 Oktober 1805 di gereja St. Catherine di Brunswick. Mereka memiliki dua putra dan satu putri: Joseph (1806-1873), Wilhelmina (1808-1840), dan Louis (1809-1810). Johanna meninggal pada 11 Oktober 1809, satu bulan setelah kelahiran Louis, yang sendiri meninggal beberapa bulan kemudian. Gauss memilih nama depan anak-anaknya untuk menghormati Giuseppe Piazzi, Wilhelm Olbers, dan Karl Ludwig Harding, para penemu asteroid pertama. Kematian Johanna sangat memukul Gauss, dan ia tidak pernah pulih sepenuhnya dari kesedihan ini.

Pada 4 Agustus 1810, Gauss menikah dengan Wilhelmine (Minna) Waldeck, seorang teman istri pertamanya, dengan siapa ia memiliki tiga anak lagi: Eugen (kemudian Eugene) (1811-1896), Wilhelm (kemudian William) (1813-1879), dan Therese (1816-1864). Minna Gauss meninggal pada 12 September 1831 setelah sakit parah selama lebih dari satu dekade. Therese kemudian mengambil alih rumah tangga dan merawat Gauss selama sisa hidupnya; setelah kematian ayahnya, ia menikah dengan aktor Constantin Staufenau. Kakaknya Wilhelmina menikah dengan orientalis Heinrich Ewald. Ibu Gauss, Dorothea, tinggal di rumahnya dari tahun 1817 hingga meninggal pada tahun 1839.

Putra sulung Joseph, saat masih sekolah, membantu ayahnya sebagai asisten selama kampanye survei pada musim panas 1821. Setelah waktu singkat di universitas, pada tahun 1824 Joseph bergabung dengan Angkatan Darat Hanover dan membantu survei lagi pada tahun 1829. Pada tahun 1830-an ia bertanggung jawab atas perluasan jaringan survei ke bagian barat kerajaan. Dengan kualifikasi geodetisnya, ia meninggalkan dinas dan terlibat dalam pembangunan jaringan kereta api sebagai direktur Royal Hanoverian State Railways. Pada tahun 1836 ia mempelajari sistem kereta api di AS selama beberapa bulan, di mana ia bertemu dengan geodesis Ferdinand Rudolph Hassler, koresponden ilmiah Carl Friedrich Gauss.

Eugen meninggalkan Göttingen pada September 1830 dan beremigrasi ke Amerika Serikat, di mana ia bergabung dengan tentara selama lima tahun. Ia kemudian bekerja untuk American Fur Company di Midwest. Kemudian, ia pindah ke Missouri dan menjadi pengusaha sukses. Eugen memiliki bakat yang baik dalam perhitungan dan bahasa seperti ayahnya, tetapi memiliki karakter yang lincah dan kadang memberontak. Ia ingin belajar filologi, sedangkan Gauss ingin ia menjadi pengacara. Setelah terlilit utang dan menyebabkan skandal di depan umum, Eugen tiba-tiba meninggalkan Göttingen dalam keadaan dramatis pada September 1830 dan beremigrasi melalui Bremen ke Amerika Serikat. Ia menghabiskan sedikit uang yang ia bawa untuk memulai, setelah itu ayahnya menolak dukungan finansial lebih lanjut.

Wilhelm menikah dengan keponakan astronom Friedrich Bessel; ia kemudian pindah ke Missouri, memulai sebagai petani dan menjadi kaya dalam bisnis sepatu di St. Louis di tahun-tahun berikutnya. Eugene dan William memiliki banyak keturunan di Amerika, tetapi keturunan Gauss yang tersisa di Jerman semuanya berasal dari Joseph, karena anak-anak perempuan tidak memiliki anak.

1.5. Kepribadian dan Keyakinan

Pada dua dekade pertama abad ke-19, Gauss adalah satu-satunya matematikawan penting di Jerman, sebanding dengan para pemimpin Prancis. Karyanya Disquisitiones Arithmeticae adalah buku matematika pertama dari Jerman yang diterjemahkan ke dalam bahasa Prancis.

Gauss "berada di garis depan perkembangan baru" dengan penelitian yang didokumentasikan sejak tahun 1799, kekayaan ide-idenya yang baru, dan ketelitian demonstrasinya. Sementara matematikawan sebelumnya seperti Leonhard Euler membiarkan pembaca mengambil bagian dalam penalaran mereka untuk ide-ide baru, termasuk penyimpangan tertentu yang salah dari jalur yang benar, Gauss memperkenalkan gaya penjelasan baru yang langsung dan lengkap yang tidak berusaha menunjukkan kepada pembaca alur pemikiran penulis.
Gauss adalah orang pertama yang mengembalikan ketelitian demonstrasi yang kita kagumi pada zaman kuno dan yang telah dipaksa terlalu jauh ke belakang oleh minat eksklusif periode sebelumnya pada perkembangan baru.
Namun, untuk dirinya sendiri, ia menyebarkan cita-cita yang sama sekali berbeda, yang diberikan dalam surat kepada Farkas Bolyai sebagai berikut:
Bukanlah pengetahuan, melainkan tindakan belajar, bukan kepemilikan melainkan tindakan mencapainya, yang memberikan kenikmatan terbesar. Ketika saya telah memperjelas dan menghabiskan suatu subjek, maka saya berpaling darinya, untuk kembali ke kegelapan.
Makalah anumerta, buku harian ilmiahnya, dan catatan singkat dalam buku teksnya sendiri menunjukkan bahwa ia bekerja secara empiris secara ekstensif. Ia adalah seorang kalkulator yang sibuk dan antusias sepanjang hidupnya, yang melakukan perhitungannya dengan kecepatan luar biasa, sebagian besar tanpa kontrol yang tepat, tetapi memeriksa hasilnya dengan perkiraan yang mahir. Meskipun demikian, perhitungannya tidak selalu bebas dari kesalahan. Ia mengatasi beban kerja yang sangat besar dengan menggunakan alat yang terampil. Gauss menggunakan banyak tabel matematika, memeriksa ketepatannya, dan membuat tabel baru tentang berbagai hal untuk penggunaan pribadi. Ia mengembangkan alat baru untuk perhitungan yang efektif, misalnya eliminasi Gauss. Telah dianggap sebagai ciri khas gaya kerjanya bahwa ia melakukan perhitungan dengan tingkat presisi yang jauh lebih tinggi dari yang dibutuhkan, dan menyiapkan tabel dengan lebih banyak tempat desimal daripada yang pernah diminta untuk tujuan praktis. Sangat mungkin, metode ini memberinya banyak materi yang ia gunakan dalam menemukan teorema dalam teori bilangan.

Gauss menolak untuk menerbitkan karya yang tidak ia anggap lengkap dan di atas kritik. Perfeksionisme ini sesuai dengan motto segel pribadinya Pauca sed Matura (Pauca sed Matura_{Sedikit, tetapi Matang}^{Bahasa Latin}). Banyak rekan mendorongnya untuk mempublikasikan ide-ide baru dan kadang-kadang menegurnya jika ia terlalu lama ragu-ragu, menurut pendapat mereka. Gauss membela diri, mengklaim bahwa penemuan awal ide-ide itu mudah, tetapi menyiapkan elaborasi yang layak disajikan adalah masalah yang menuntut baginya, baik karena kurangnya waktu atau "ketenangan pikiran". Meskipun demikian, ia menerbitkan banyak komunikasi singkat tentang konten mendesak di berbagai jurnal, tetapi juga meninggalkan warisan sastra yang cukup besar. Gauss menyebut matematika sebagai "ratu ilmu pengetahuan" dan aritmetika sebagai "ratu matematika", dan konon pernah menganut keyakinan akan perlunya segera memahami identitas Euler sebagai tolok ukur untuk menjadi matematikawan kelas satu.

Pada kesempatan tertentu, Gauss mengklaim bahwa ide-ide cendekiawan lain sudah ia miliki sebelumnya. Dengan demikian, konsep prioritasnya sebagai "yang pertama menemukan, bukan yang pertama menerbitkan" berbeda dari rekan-rekan ilmiahnya. Berbeda dengan perfeksionismenya dalam menyajikan ide-ide matematika, ia dikritik karena cara mengutip yang lalai. Ia membenarkan dirinya dengan pandangan yang sangat khusus tentang kutipan yang benar: jika ia memberikan referensi, maka hanya dengan cara yang sangat lengkap, sehubungan dengan penulis-penulis penting sebelumnya, yang tidak boleh diabaikan; tetapi mengutip dengan cara ini membutuhkan pengetahuan tentang sejarah sains dan lebih banyak waktu daripada yang ia inginkan.

Tak lama setelah kematian Gauss, temannya Sartorius menerbitkan biografi pertama (1856), yang ditulis dengan gaya yang agak antusias. Sartorius melihatnya sebagai pria yang tenang dan maju dengan kerendahan hati seperti anak kecil, tetapi juga memiliki "karakter baja" dengan kekuatan pikiran yang tak tergoyahkan. Selain lingkaran dekatnya, orang lain menganggapnya sebagai "seorang Olympian yang duduk bertakhta di puncak ilmu pengetahuan" yang pendiam dan tidak mudah didekati. Rekan-rekan sezamannya yang dekat sepakat bahwa Gauss adalah pria dengan karakter yang sulit. Ia sering menolak menerima pujian. Para pengunjungnya kadang-kadang kesal dengan perilakunya yang pemarah, tetapi tak lama kemudian suasana hatinya bisa berubah, dan ia akan menjadi tuan rumah yang menawan dan berpikiran terbuka. Gauss membenci sifat-sifat polemik; bersama dengan rekannya Hausmann ia menentang panggilan untuk Justus Liebig di kursi universitas di Göttingen, "karena ia selalu terlibat dalam beberapa polemik."

Kehidupan Gauss dibayangi oleh masalah serius dalam keluarganya. Ketika istri pertamanya Johanna tiba-tiba meninggal tak lama setelah kelahiran anak ketiga mereka, ia mengungkapkan kesedihan dalam surat terakhir kepada istrinya yang meninggal dalam gaya threnody kuno, dokumen paling pribadi yang bertahan dari Gauss. Situasi memburuk ketika tuberkulosis akhirnya menghancurkan kesehatan istri keduanya Minna selama 13 tahun; kedua putrinya kemudian menderita penyakit yang sama. Gauss sendiri hanya memberikan sedikit petunjuk tentang kesusahannya: dalam surat kepada Bessel bertanggal Desember 1831 ia menggambarkan dirinya sebagai "korban penderitaan rumah tangga terburuk".

Karena penyakit istrinya, kedua putra bungsunya dididik selama beberapa tahun di Celle, jauh dari Göttingen. Karier militer putra sulungnya Joseph berakhir setelah lebih dari dua dekade dengan pangkat letnan satu yang bergaji rendah, meskipun ia telah memperoleh pengetahuan geodesi yang cukup besar. Ia membutuhkan dukungan finansial dari ayahnya bahkan setelah ia menikah. Putra kedua Eugen memiliki bakat yang baik dalam perhitungan dan bahasa seperti ayahnya, tetapi memiliki karakter yang lincah dan kadang memberontak. Ia ingin belajar filologi, sedangkan Gauss ingin ia menjadi pengacara. Setelah terlilit utang dan menyebabkan skandal di depan umum, Eugen tiba-tiba meninggalkan Göttingen dalam keadaan dramatis pada September 1830 dan beremigrasi melalui Bremen ke Amerika Serikat. Ia menghabiskan sedikit uang yang ia bawa untuk memulai, setelah itu ayahnya menolak dukungan finansial lebih lanjut. Putra bungsu Wilhelm ingin memenuhi syarat untuk administrasi pertanian, tetapi mengalami kesulitan mendapatkan pendidikan yang sesuai, dan akhirnya beremigrasi juga. Hanya putri bungsu Gauss, Therese, yang menemaninya di tahun-tahun terakhir hidupnya.

Mengumpulkan data numerik tentang berbagai hal yang sangat berbeda, berguna atau tidak berguna, menjadi kebiasaan di tahun-tahun terakhirnya, misalnya, jumlah jalur dari rumahnya ke tempat-tempat tertentu di Göttingen, atau jumlah hari hidup seseorang; ia mengucapkan selamat kepada Humboldt pada Desember 1851 karena telah mencapai usia yang sama dengan Isaac Newton saat kematiannya, dihitung dalam hari.

Mirip dengan pengetahuannya yang sangat baik tentang Latin, ia juga akrab dengan bahasa-bahasa modern. Pada usia 62 tahun, ia mulai belajar bahasa Rusia sendiri, sangat mungkin untuk memahami tulisan-tulisan ilmiah dari Rusia, di antaranya adalah tulisan Lobachevsky tentang geometri non-Euclidean. Gauss membaca sastra klasik dan modern, serta karya-karya Inggris dan Prancis dalam bahasa aslinya. Buku pertama yang ia pinjam dari perpustakaan universitas pada tahun 1795 adalah novel Clarissa dari Samuel Richardson. Penulis Inggris favoritnya adalah Walter Scott, favorit Jermannya Jean Paul. Gauss suka bernyanyi dan pergi ke konser. Ia adalah pembaca surat kabar yang rajin; di tahun-tahun terakhirnya, ia biasa mengunjungi salon pers akademik universitas setiap siang. Gauss tidak terlalu peduli dengan filsafat, dan mengejek "pemecahan rambut dari apa yang disebut metafisikawan", yang ia maksud adalah para pendukung aliran kontemporer Naturphilosophie.

Gauss memiliki "sifat aristokrat dan konservatif secara menyeluruh", dengan sedikit rasa hormat terhadap kecerdasan dan moral orang, mengikuti motto "mundus vult decipi". Ia tidak menyukai Napoleon dan sistemnya, dan segala jenis kekerasan serta revolusi menyebabkan kengerian baginya. Dengan demikian, ia mengutuk metode Revolusi 1848, meskipun ia setuju dengan beberapa tujuannya, seperti gagasan Jerman yang bersatu. Sejauh menyangkut sistem politik, ia memiliki estimasi rendah terhadap sistem konstitusional; ia mengkritik anggota parlemen pada masanya karena kurangnya pengetahuan dan kesalahan logis.

Beberapa biografer Gauss berspekulasi tentang keyakinan agamanya. Ia kadang-kadang berkata "Tuhan mengaritmetika" dan "Saya berhasil - bukan karena usaha keras saya, tetapi oleh anugerah Tuhan." Gauss adalah anggota Gereja Lutheran, seperti sebagian besar penduduk di Jerman utara. Tampaknya ia tidak mempercayai semua dogma atau memahami Alkitab secara harfiah. Sartorius menyebutkan toleransi beragama Gauss, dan memperkirakan "dahaga tak terpuaskan akan kebenaran" dan rasa keadilannya dimotivasi oleh keyakinan agama. Ia percaya bahwa ilmu pengetahuan adalah cara untuk mengungkapkan inti abadi dari jiwa manusia, dan bahwa wahyu Tuhan bersifat berkelanjutan. Ia juga memiliki keyakinan kuat pada kehidupan setelah kematian.

1.6. Otak Gauss

Sehari setelah kematian Gauss, otaknya diangkat, diawetkan, dan dipelajari oleh Rudolf Wagner, yang menemukan massanya sedikit di atas rata-rata, yaitu 1.49 K g. Putra Wagner, Hermann, seorang ahli geografi, memperkirakan area serebralnya sebesar 219.59 K mm². Pada tahun 2013, seorang neurobiolog di Max Planck Institute for Biophysical Chemistry di Göttingen menemukan bahwa otak Gauss telah tertukar tak lama setelah penyelidikan pertama, karena salah label, dengan otak dokter Conrad Heinrich Fuchs, yang meninggal di Göttingen beberapa bulan setelah Gauss. Penyelidikan lebih lanjut menunjukkan tidak ada anomali yang luar biasa pada otak kedua orang tersebut. Dengan demikian, semua penyelidikan terhadap otak Gauss hingga tahun 1998, kecuali yang pertama oleh Rudolf dan Hermann Wagner, sebenarnya merujuk pada otak Fuchs.

1.7. Kematian dan Warisan

Gauss tetap aktif secara mental hingga usia tuanya, meskipun menderita gout dan ketidakbahagiaan umum. Pada 23 Februari 1855, ia meninggal karena serangan jantung di Göttingen; dan dimakamkan di Pemakaman Albani di sana. Heinrich Ewald, menantu Gauss, dan Wolfgang Sartorius von Waltershausen, teman dekat dan biografer Gauss, memberikan eulogi pada pemakamannya.

Gauss adalah investor yang sukses dan mengumpulkan kekayaan yang cukup besar dengan saham dan sekuritas, akhirnya bernilai lebih dari 150 ribu Thaler; setelah kematiannya, sekitar 18 ribu Thaler ditemukan tersembunyi di kamarnya.

2.1. Matematika

Kontribusi Gauss dalam berbagai cabang matematika menunjukkan keluasan dan kedalaman pemikirannya yang luar biasa, meletakkan dasar bagi banyak bidang modern.

2.2. Analisis

Salah satu penemuan pertama Gauss adalah gagasan rata-rata aritmetika-geometris (AGM) dari dua bilangan riil positif. Ia menemukan hubungannya dengan integral eliptik pada tahun 1798-1799 melalui transformasi Landen, dan entri buku harian mencatat penemuan hubungan konstanta Gauss dengan fungsi eliptik lemniskat, sebuah hasil yang Gauss nyatakan bahwa "pasti akan membuka bidang analisis yang sama sekali baru". Ia juga membuat terobosan awal ke dalam masalah yang lebih formal tentang dasar-dasar analisis kompleks, dan dari surat kepada Bessel pada tahun 1811 jelas bahwa ia mengetahui "teorema fundamental analisis kompleks" - teorema integral Cauchy - dan memahami gagasan residu kompleks ketika mengintegrasikan di sekitar kutub.

Teorema bilangan pentagonal Euler, bersama dengan penelitian lain tentang AGM dan fungsi lemniskat, membawanya ke banyak hasil tentang fungsi theta Jacobi, yang berpuncak pada penemuan pada tahun 1808 dari identitas produk rangkap tiga Jacobi yang kemudian disebut, yang mencakup teorema Euler sebagai kasus khusus. Karya-karyanya menunjukkan bahwa ia mengetahui transformasi modular orde 3, 5, 7 untuk fungsi eliptik sejak tahun 1808.

Beberapa fragmen matematika dalam Nachlass-nya menunjukkan bahwa ia mengetahui bagian-bagian dari teori modern bentuk modular. Dalam karyanya tentang AGM bernilai banyak dari dua bilangan kompleks, ia menemukan hubungan yang mendalam antara nilai-nilai AGM yang tak terbatas dengan dua "nilai paling sederhana"-nya. Dalam tulisan-tulisan yang tidak diterbitkan, ia mengenali dan membuat sketsa konsep kunci domain fundamental untuk grup modular. Salah satu sketsa Gauss semacam ini adalah gambar tessellasi dari cakram unit oleh segitiga hiperbolik "ekilateral" dengan semua sudut sama dengan pi/4.

Contoh wawasan Gauss dalam bidang analisis adalah pernyataan samar bahwa prinsip-prinsip pembagian lingkaran dengan kompas dan penggaris juga dapat diterapkan pada pembagian kurva lemniskat, yang menginspirasi teorema Abel tentang pembagian lemniskat. Contoh lain adalah publikasinya "Summatio quarundam serierum singularium" (1811) tentang penentuan tanda jumlah Gauss kuadratik, di mana ia memecahkan masalah utama dengan memperkenalkan q-analog koefisien binomial dan memanipulasinya dengan beberapa identitas asli yang tampaknya berasal dari karyanya tentang teori fungsi eliptik; namun, Gauss menyajikan argumennya secara formal yang tidak mengungkapkan asalnya dalam teori fungsi eliptik, dan hanya karya matematikawan selanjutnya seperti Jacobi dan Hermite yang telah mengungkapkan inti argumennya.

Dalam "Disquisitiones generales circa series infinitam..." (1813), ia memberikan perlakuan sistematis pertama dari fungsi hipergeometrik umum F(α,β,γ,x), dan menunjukkan bahwa banyak fungsi yang dikenal pada saat itu adalah kasus khusus dari fungsi hipergeometrik. Karya ini adalah yang pertama dengan penyelidikan yang tepat tentang konvergensi deret tak terbatas dalam sejarah matematika. Selanjutnya, ini membahas pecahan berlanjut tak terbatas yang muncul sebagai rasio fungsi hipergeometrik yang sekarang disebut pecahan berlanjut Gauss.

Pada tahun 1823, Gauss memenangkan hadiah dari Masyarakat Denmark dengan esai tentang pemetaan konformal, yang berisi beberapa perkembangan yang berkaitan dengan bidang analisis kompleks. Gauss menyatakan bahwa pemetaan yang mempertahankan sudut dalam bidang kompleks harus berupa fungsi analitik kompleks, dan menggunakan persamaan Beltrami yang kemudian disebut untuk membuktikan keberadaan koordinat isotermal pada permukaan analitik. Esai tersebut diakhiri dengan contoh pemetaan konformal ke dalam bola dan elipsoid revolusi.

2.3. Geometri Diferensial

Survei geodetik Hanover memicu minat Gauss pada geometri diferensial dan topologi, bidang matematika yang berhubungan dengan kurva dan permukaan. Ini membawanya pada tahun 1828 untuk menerbitkan sebuah memoar yang menandai lahirnya geometri diferensial permukaan modern, karena ia menyimpang dari cara-cara tradisional dalam memperlakukan permukaan sebagai grafik Kartesius dari fungsi dua variabel, dan yang memulai eksplorasi permukaan dari sudut pandang "internal" makhluk dua dimensi yang terbatas untuk bergerak di atasnya. Akibatnya, Theorema Egregium (teorema yang luar biasa), menetapkan properti dari gagasan kelengkungan Gauss. Secara informal, teorema tersebut mengatakan bahwa kelengkungan suatu permukaan dapat ditentukan sepenuhnya dengan mengukur sudut dan jarak pada permukaan, terlepas dari embedding permukaan dalam ruang tiga dimensi atau dua dimensi.

Theorema Egregium mengarah pada abstraksi permukaan sebagai manifold yang diperluas ganda; ini memperjelas perbedaan antara sifat intrinsik manifold (metrik) dan realisasi fisiknya dalam ruang ambien. Konsekuensinya adalah ketidakmungkinan transformasi isometrik antara permukaan dengan kelengkungan Gaussian yang berbeda. Ini berarti secara praktis bahwa bola atau elipsoid tidak dapat diubah menjadi bidang tanpa distorsi, yang menyebabkan masalah fundamental dalam merancang proyeksi peta untuk peta geografis. Sebagian dari esai ini didedikasikan untuk studi mendalam tentang geodesik. Secara khusus, Gauss membuktikan teorema Gauss-Bonnet lokal pada segitiga geodesik, dan menggeneralisasi teorema Legendre tentang segitiga bola ke segitiga geodesik pada permukaan arbitrer dengan kelengkungan kontinu; ia menemukan bahwa sudut-sudut segitiga geodesik "yang cukup kecil" menyimpang dari segitiga planar dengan sisi yang sama dengan cara yang hanya bergantung pada nilai kelengkungan permukaan pada simpul-simpul segitiga, terlepas dari perilaku permukaan di interior segitiga.

Memoar Gauss dari tahun 1828 tidak memiliki konsep kelengkungan geodesik. Namun, dalam manuskrip yang sebelumnya tidak diterbitkan, kemungkinan besar ditulis pada tahun 1822-1825, ia memperkenalkan istilah "kelengkungan sisi" (Jerman: "Seitenkrümmung") dan membuktikan invariansinya di bawah transformasi isometrik, sebuah hasil yang kemudian diperoleh oleh Ferdinand Minding dan diterbitkan olehnya pada tahun 1830. Makalah Gauss ini berisi inti dari lema tentang kelengkungan total, tetapi juga generalisasinya, yang ditemukan dan dibuktikan oleh Pierre Ossian Bonnet pada tahun 1848 dan dikenal sebagai teorema Gauss-Bonnet.

2.4. Geometri Non-Euclidean

Selama hidup Gauss, terjadi diskusi yang hidup tentang postulat paralel dalam geometri Euclidean. Banyak upaya dilakukan untuk membuktikannya dalam kerangka aksioma Euclidean, sementara beberapa matematikawan membahas kemungkinan sistem geometris tanpanya. Gauss memikirkan dasar-dasar geometri sejak tahun 1790-an, tetapi pada tahun 1810-an ia menyadari bahwa geometri non-Euclidean tanpa postulat paralel dapat memecahkan masalah tersebut. Dalam surat kepada Franz Taurinus pada tahun 1824, ia menyajikan garis besar singkat yang mudah dipahami tentang apa yang ia sebut "geometri non-Euclidean", tetapi ia sangat melarang Taurinus untuk menggunakannya. Gauss dikreditkan sebagai orang pertama yang menemukan dan mempelajari geometri non-Euclidean, bahkan menciptakan istilah tersebut.

Publikasi pertama tentang geometri non-Euclidean dalam sejarah matematika ditulis oleh Nikolai Lobachevsky pada tahun 1829 dan Janos Bolyai pada tahun 1832. Pada tahun-tahun berikutnya, Gauss menulis ide-idenya tentang topik tersebut tetapi tidak mempublikasikannya, sehingga menghindari pengaruh diskusi ilmiah kontemporer. Gauss memuji ide-idenya Janos Bolyai dalam surat kepada ayahnya dan teman universitasnya Farkas Bolyai, mengklaim bahwa ini sesuai dengan pemikirannya sendiri selama beberapa dekade. Namun, tidak sepenuhnya jelas sejauh mana ia mendahului Lobachevsky dan Bolyai, karena catatan suratnya hanya samar dan tidak jelas.

Sartorius menyebutkan karya Gauss tentang geometri non-Euclidean pertama kali pada tahun 1856, tetapi hanya edisi makalah yang ditinggalkan dalam Volume VIII dari Collected Works (1900) yang menunjukkan ide-ide Gauss tentang masalah itu, pada saat geometri non-Euclidean belum tumbuh dari diskusi kontroversial.

2.5. Topologi Awal

Gauss juga merupakan pelopor awal topologi atau Geometria Situs, sebagaimana disebut pada masanya. Bukti pertama teorema dasar aljabar pada tahun 1799 berisi argumen yang pada dasarnya topologis; lima puluh tahun kemudian, ia lebih lanjut mengembangkan argumen topologis dalam bukti keempatnya tentang teorema ini.

Perjumpaan lain dengan gagasan topologis terjadi padanya dalam pekerjaannya di bidang astronomi pada tahun 1804, ketika ia menentukan batas-batas wilayah di bola langit di mana komet dan asteroid mungkin muncul, dan yang ia sebut "Zodiacus". Ia menemukan bahwa jika orbit Bumi dan komet terkait, maka karena alasan topologis Zodiacus adalah seluruh bola. Pada tahun 1848, dalam konteks penemuan asteroid 7 Iris, ia menerbitkan diskusi kualitatif lebih lanjut tentang Zodiacus.

Dalam surat-surat Gauss tahun 1820-1830, ia berpikir secara intensif tentang topik-topik yang sangat erat kaitannya dengan Geometria Situs, dan secara bertahap menyadari kesulitan semantik di bidang ini. Fragmen dari periode ini mengungkapkan bahwa ia mencoba mengklasifikasikan "gambar traktat", yaitu kurva bidang tertutup dengan sejumlah terbatas persimpangan diri transversal, yang mungkin juga merupakan proyeksi planar dari simpul. Untuk melakukannya, ia merancang skema simbolis, kode Gauss, yang dalam arti tertentu menangkap fitur-fitur karakteristik gambar traktat.

Dalam fragmen dari tahun 1833, Gauss mendefinisikan bilangan penghubung dari dua kurva ruang dengan integral ganda tertentu, dan dengan demikian memberikan untuk pertama kalinya formulasi analitis dari fenomena topologis. Pada catatan yang sama, ia meratapi sedikit kemajuan yang dicapai dalam Geometria Situs, dan menyatakan bahwa salah satu masalah sentralnya adalah "menghitung jalinan dua kurva tertutup atau tak terbatas". Buku catatannya dari periode itu mengungkapkan bahwa ia juga memikirkan objek topologis lain seperti jalinan dan kusut.

Pengaruh Gauss di tahun-tahun berikutnya terhadap bidang topologi yang baru muncul, yang sangat ia hargai, adalah melalui catatan sesekali dan komunikasi lisan kepada Mobius dan Listing.

2.6. Pencapaian Matematika Minor

Gauss menerapkan konsep bilangan kompleks untuk memecahkan masalah-masalah terkenal dengan cara baru yang ringkas. Misalnya, dalam catatan singkat dari tahun 1836 tentang aspek geometris bentuk terner dan penerapannya pada kristalografi, ia menyatakan teorema dasar aksonometri, yang menjelaskan cara merepresentasikan kubus 3D pada bidang 2D dengan akurasi lengkap, melalui bilangan kompleks. Ia menggambarkan rotasi bola ini sebagai tindakan transformasi pecahan linear tertentu pada bidang kompleks yang diperluas, dan memberikan bukti untuk teorema geometris bahwa ketinggian segitiga selalu bertemu di satu ortosenter.

Gauss tertarik pada "Pentagramma mirificum" John Napier - sebuah pentagram bola tertentu - selama beberapa dekade; ia mendekatinya dari berbagai sudut pandang, dan secara bertahap memperoleh pemahaman penuh tentang aspek geometris, aljabar, dan analitisnya. Secara khusus, pada tahun 1843 ia menyatakan dan membuktikan beberapa teorema yang menghubungkan fungsi eliptik, pentagon bola Napier, dan pentagon Poncelet di bidang.

Selanjutnya, ia memberikan solusi untuk masalah membangun elips dengan area terbesar di dalam segi empat yang diberikan, dan menemukan hasil yang mengejutkan tentang perhitungan area pentagon.

2.7. Astronomi

Kontribusi Gauss di bidang astronomi, mulai dari penemuan Ceres hingga pengembangan teori orbit dan perhitungan yang akurat, menunjukkan keahliannya yang luar biasa dalam mekanika benda langit.

2.8. Teori Kesalahan

Gauss kemungkinan menggunakan metode kuadrat terkecil untuk menghitung orbit Ceres guna meminimalkan dampak kesalahan pengukuran. Metode ini pertama kali diterbitkan oleh Adrien-Marie Legendre pada tahun 1805, tetapi Gauss mengklaim dalam Theoria motus (1809) bahwa ia telah menggunakannya sejak tahun 1794 atau 1795. Dalam sejarah statistik, perselisihan ini disebut "sengketa prioritas atas penemuan metode kuadrat terkecil". Gauss membuktikan bahwa metode ini memiliki varians sampling terendah dalam kelas estimator linear tak bias di bawah asumsi kesalahan terdistribusi normal (teorema Gauss-Markov), dalam makalah dua bagian Theoria combinationis observationum erroribus minimis obnoxiae (1823).

Dalam makalah pertama ia membuktikan ketidaksetaraan Gauss (ketidaksetaraan tipe Chebyshev) untuk distribusi unimodal, dan menyatakan tanpa bukti ketidaksetaraan lain untuk momen orde keempat (kasus khusus dari ketidaksetaraan Gauss-Winckler). Ia menurunkan batas bawah dan atas untuk varians dari varians sampel. Dalam makalah kedua, Gauss menjelaskan metode kuadrat terkecil rekursif. Karyanya tentang teori kesalahan diperluas ke beberapa arah oleh geodesis Friedrich Robert Helmert ke model Gauss-Helmert.

Gauss juga berkontribusi pada masalah dalam teori probabilitas yang tidak secara langsung berkaitan dengan teori kesalahan. Salah satu contoh muncul sebagai catatan buku harian di mana ia mencoba menggambarkan distribusi asimtotik entri dalam ekspansi pecahan berlanjut dari bilangan acak yang terdistribusi seragam di (0,1). Ia menurunkan distribusi ini, yang sekarang dikenal sebagai distribusi Gauss-Kuzmin, sebagai produk sampingan dari penemuan ergodisitas dari peta Gauss untuk pecahan berlanjut. Solusi Gauss adalah hasil pertama dalam teori metrik pecahan berlanjut.

2.9. Pengukuran Busur dan Survei Geodetik

Gauss sibuk dengan masalah geodetik sejak tahun 1799 ketika ia membantu Karl Ludwig von Lecoq dengan perhitungan selama surveinya di Westphalia. Mulai tahun 1804, ia belajar sendiri beberapa praktik geodetik dengan sextan di Brunswick, dan Göttingen.

Sejak tahun 1816, mantan mahasiswa Gauss, Heinrich Christian Schumacher, yang saat itu profesor di Kopenhagen, tetapi tinggal di Altona (Holstein) dekat Hamburg sebagai kepala observatorium, melakukan triangulasi semenanjung Jutland dari Skagen di utara hingga Lauenburg di selatan. Proyek ini adalah dasar untuk produksi peta tetapi juga bertujuan untuk menentukan busur geodetik antara situs terminal. Data dari busur geodetik digunakan untuk menentukan dimensi geoid bumi, dan jarak busur yang panjang menghasilkan hasil yang lebih tepat. Schumacher meminta Gauss untuk melanjutkan pekerjaan ini lebih jauh ke selatan di Kerajaan Hanover; Gauss setuju setelah ragu-ragu sebentar. Akhirnya, pada Mei 1820, Raja George IV memberikan perintah kepada Gauss.

Pengukuran busur membutuhkan penentuan astronomi yang tepat dari setidaknya dua titik dalam jaringan triangulasi. Gauss dan Schumacher memanfaatkan kesempatan yang menguntungkan bahwa kedua observatorium di Göttingen dan Altona, di taman rumah Schumacher, terletak hampir pada bujur yang sama. Lintang diukur dengan kedua instrumen mereka dan sektor zenit Ramsden yang diangkut ke kedua observatorium.

Gauss dan Schumacher telah menentukan beberapa sudut antara Lüneburg, Hamburg, dan Lauenburg untuk koneksi geodetik pada Oktober 1818. Selama musim panas 1821 hingga 1825 Gauss secara pribadi mengarahkan pekerjaan triangulasi, dari Thuringia di selatan hingga sungai Elbe di utara. Segitiga antara Hoher Hagen, Großer Inselsberg di Hutan Thuringian, dan Brocken di pegunungan Harz adalah yang terbesar yang pernah diukur Gauss dengan ukuran maksimum 107 km. Di Lüneburg Heath yang jarang penduduknya tanpa puncak alami yang signifikan atau bangunan buatan, ia mengalami kesulitan menemukan titik triangulasi yang cocok; kadang-kadang diperlukan untuk memotong jalur melalui vegetasi.

Untuk menunjukkan sinyal, Gauss menemukan instrumen baru dengan cermin bergerak dan teleskop kecil yang memantulkan sinar matahari ke titik-titik triangulasi, dan menamakannya heliotrop. Konstruksi lain yang cocok untuk tujuan yang sama adalah sextan dengan cermin tambahan yang ia namakan wakil heliotrop. Gauss mendapat bantuan dari tentara Hanoverian, di antaranya putra sulungnya Joseph. Gauss mengambil bagian dalam pengukuran garis dasar (Braak Base Line) Schumacher di desa Braak dekat Hamburg pada tahun 1820, dan menggunakan hasilnya untuk evaluasi triangulasi Hanoverian.

Hasil tambahan adalah nilai pemipihan yang lebih baik dari elipsoid Bumi perkiraan. Gauss mengembangkan proyeksi Transverse Mercator Universal dari Bumi berbentuk elipsoid (yang ia namakan proyeksi konform) untuk merepresentasikan data geodetik dalam peta datar.

Ketika pengukuran busur selesai, Gauss memulai perluasan triangulasi ke barat untuk mendapatkan survei seluruh Kerajaan Hanover dengan dekrit Kerajaan dari 25 Maret 1828. Pekerjaan praktis diarahkan oleh tiga perwira militer, di antaranya Letnan Joseph Gauss. Evaluasi data lengkap berada di tangan Gauss, yang menerapkan penemuan matematikanya seperti metode kuadrat terkecil dan metode eliminasi Gauss padanya. Proyek ini selesai pada tahun 1844, dan Gauss mengirimkan laporan akhir proyek kepada pemerintah; metode proyeksinya tidak diedit hingga tahun 1866.

Pada tahun 1828, ketika mempelajari perbedaan lintang, Gauss pertama kali mendefinisikan perkiraan fisik untuk bentuk Bumi sebagai permukaan yang di setiap titik tegak lurus terhadap arah gravitasi; kemudian mahasiswa doktoralnya Johann Benedict Listing menyebut ini geoid.

2.10. Fisika

Kontribusi Gauss di berbagai bidang fisika, mulai dari magnetisme hingga optik, menunjukkan pemahamannya yang mendalam tentang fenomena alam.

2.10.1. Geomagnetisme

Gauss telah tertarik pada magnetisme sejak tahun 1803. Setelah Alexander von Humboldt mengunjungi Göttingen pada tahun 1826, kedua ilmuwan tersebut memulai penelitian intensif tentang geomagnetisme, sebagian secara independen, sebagian dalam kerja sama yang produktif. Pada tahun 1828, Gauss adalah tamu Humboldt selama konferensi Society of German Natural Scientists and Physicians di Berlin, di mana ia berkenalan dengan fisikawan Wilhelm Weber.

Ketika Weber mendapatkan kursi fisika di Göttingen sebagai penerus Johann Tobias Mayer atas rekomendasi Gauss pada tahun 1831, keduanya memulai kolaborasi yang bermanfaat, yang mengarah pada pengetahuan baru tentang magnetisme dengan representasi untuk satuan magnetisme dalam hal massa, muatan, dan waktu. Mereka mendirikan Asosiasi Magnetik (Jerman: Magnetischer Verein), sebuah kelompok kerja internasional dari beberapa observatorium, yang mendukung pengukuran medan magnet Bumi di banyak wilayah di dunia dengan metode yang sama pada tanggal yang disepakati pada tahun 1836 hingga 1841.

Pada tahun 1836, Humboldt menyarankan pembentukan jaringan stasiun geomagnetik di seluruh dunia di wilayah kekuasaan Britania dengan surat kepada Adipati Sussex, yang saat itu menjabat sebagai presiden Royal Society; ia mengusulkan agar pengukuran magnetik dilakukan di bawah kondisi standar menggunakan metodenya. Bersama dengan pemicu lainnya, ini mengarah pada program global yang dikenal sebagai "Perang Salib Magnetik" di bawah arahan Edward Sabine. Tanggal, waktu, dan interval observasi ditentukan sebelumnya, waktu rata-rata Göttingen digunakan sebagai standar. 61 stasiun di kelima benua berpartisipasi dalam program global ini. Gauss dan Weber mendirikan seri publikasi hasil, enam volume diedit antara tahun 1837 dan 1843. Kepergian Weber ke Leipzig pada tahun 1843 sebagai efek lanjutan dari urusan Tujuh Göttingen menandai berakhirnya aktivitas Asosiasi Magnetik.

Mengikuti contoh Humboldt, Gauss memerintahkan pembangunan observatorium magnetik di taman observatorium, tetapi para ilmuwan berbeda pendapat mengenai peralatan instrumen; Gauss lebih menyukai instrumen stasioner, yang menurutnya memberikan hasil yang lebih tepat, sedangkan Humboldt terbiasa dengan instrumen bergerak. Gauss tertarik pada variasi temporal dan spasial deklinasi, inklinasi, dan intensitas magnetik, tetapi membedakan konsep intensitas magnetik Humboldt dengan istilah intensitas "horizontal" dan "vertikal". Bersama dengan Weber, ia mengembangkan metode pengukuran komponen intensitas medan magnet dan membangun magnetometer yang cocok untuk mengukur nilai absolut kekuatan medan magnet Bumi, bukan lagi nilai relatif yang bergantung pada aparat. Presisi magnetometer sekitar sepuluh kali lebih tinggi dari instrumen sebelumnya. Dengan karya ini, Gauss adalah orang pertama yang menurunkan kuantitas non-mekanik dari kuantitas mekanik dasar.

Gauss melakukan Teori Umum Magnetisme Terestrial (1839), di mana ia percaya dapat menggambarkan sifat gaya magnet; menurut Felix Klein, karya ini adalah presentasi observasi dengan menggunakan harmonik bola daripada teori fisik. Teori tersebut memprediksi keberadaan tepat dua kutub magnetik di Bumi, sehingga gagasan Hansteen tentang empat kutub magnetik menjadi usang, dan data memungkinkan untuk menentukan lokasinya dengan presisi yang cukup baik.

Gauss memengaruhi awal geofisika di Rusia, ketika Adolph Theodor Kupffer, salah satu mantan mahasiswanya, mendirikan observatorium magnetik di St. Petersburg, mengikuti contoh observatorium di Göttingen, dan demikian pula, Ivan Simonov di Kazan.

2.10.2. Elektromagnetisme

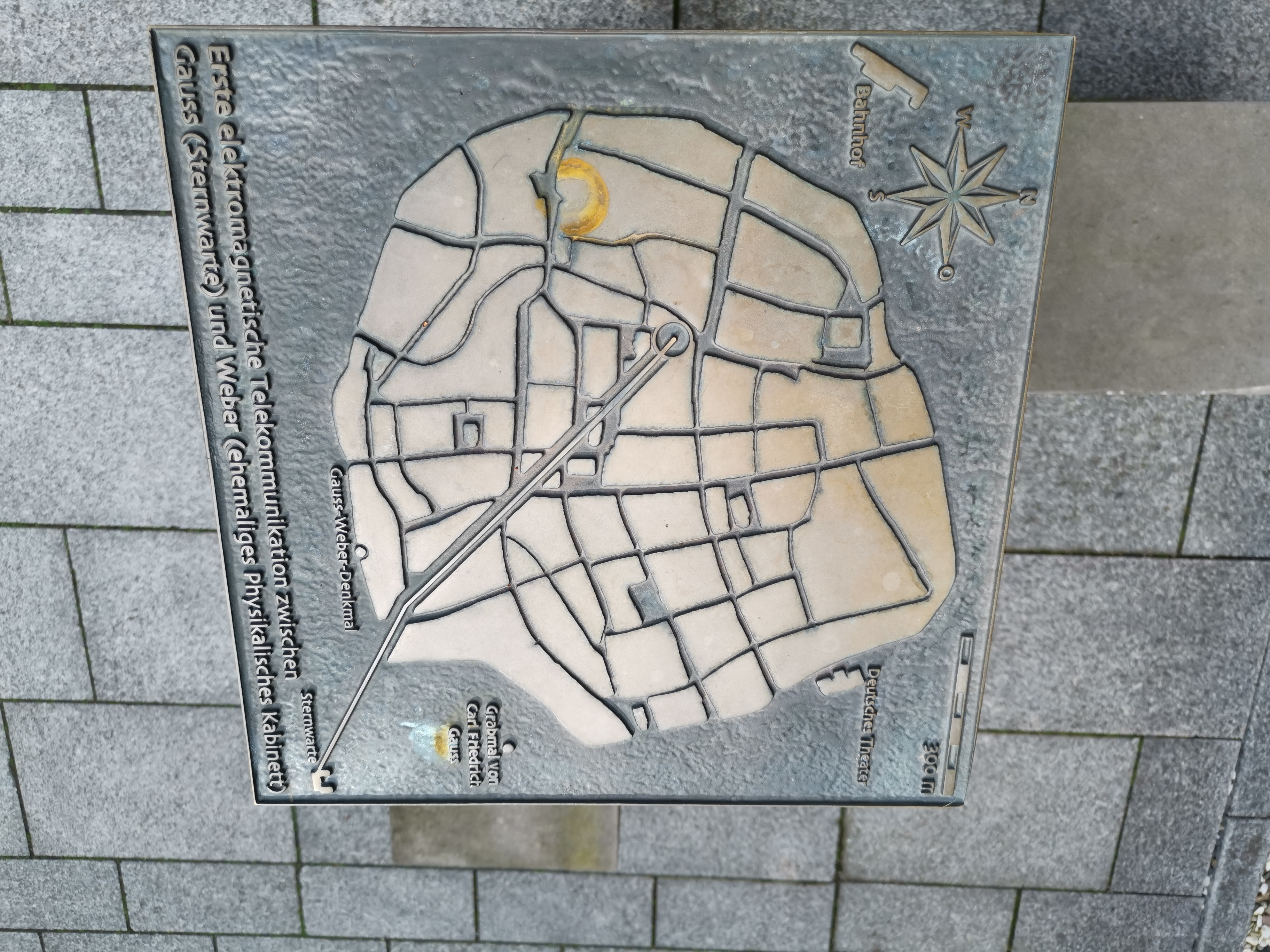
Penemuan Hans Christian Ørsted tentang elektromagnetisme dan Michael Faraday tentang induksi elektromagnetik menarik perhatian Gauss pada masalah ini. Gauss dan Weber menemukan aturan untuk sirkuit listrik bercabang, yang kemudian ditemukan secara independen dan pertama kali diterbitkan oleh Gustav Kirchhoff dan dinamai menurut namanya sebagai hukum sirkuit Kirchhoff, dan melakukan penyelidikan tentang elektromagnetisme. Mereka membangun telegraf elektromagnetik pertama pada tahun 1833, dan Weber sendiri menghubungkan observatorium dengan institut fisika di pusat kota Göttingen, tetapi mereka tidak peduli dengan pengembangan lebih lanjut dari penemuan ini untuk tujuan komersial.

Minat teoritis utama Gauss dalam elektromagnetisme tercermin dalam upayanya untuk merumuskan hukum kuantitatif yang mengatur induksi elektromagnetik. Dalam buku catatan dari tahun-tahun ini, ia mencatat beberapa formulasi inovatif; ia menemukan gagasan fungsi potensial vektor (ditemukan kembali secara independen oleh Franz Ernst Neumann pada tahun 1845), dan pada Januari 1835 ia menuliskan "hukum induksi" yang setara dengan hukum induksi Faraday, yang menyatakan bahwa gaya gerak listrik pada titik tertentu dalam ruang sama dengan laju perubahan sesaat (terhadap waktu) dari fungsi ini.

Gauss mencoba menemukan hukum pemersatu untuk efek jarak jauh elektrostatika, elektrodinamika, elektromagnetisme, dan induksi listrik, sebanding dengan hukum gravitasi Newton, tetapi upayanya berakhir dengan "kegagalan tragis".

2.11. Kronologi

Publikasi pertama setelah tesis doktoral membahas penentuan tanggal Paskah (1800), masalah matematika dasar. Gauss bertujuan untuk menyajikan algoritma yang paling nyaman bagi orang-orang tanpa pengetahuan tentang kronologi gerejawi atau bahkan astronomi, dan dengan demikian menghindari istilah yang biasanya diperlukan seperti angka emas, epact, siklus matahari, huruf domenikal, dan konotasi agama apa pun. Para biografer berspekulasi tentang alasan mengapa Gauss menangani masalah ini, tetapi kemungkinan besar dapat dipahami dari latar belakang sejarah. Penggantian kalender Julian dengan kalender Gregorian telah menyebabkan kebingungan di Kekaisaran Romawi Suci sejak abad ke-16 dan tidak selesai di Jerman sampai tahun 1700 ketika perbedaan sebelas hari dihapus, tetapi perbedaan dalam menghitung tanggal Paskah tetap ada antara wilayah Protestan dan Katolik. Perjanjian lebih lanjut tahun 1776 menyamakan cara penghitungan pengakuan dosa; jadi di negara-negara Protestan seperti Kadipaten Brunswick, Paskah tahun 1777, lima minggu sebelum kelahiran Gauss, adalah yang pertama dihitung dengan cara baru.

4.1. Matematika dan Astronomi

• 1799: Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse (Tesis doktoral tentang teorema dasar aljabar, Universitas Helmstedt)
• 1800: Berechnung des Osterfestes (Perhitungan Paskah)
• 1801: Disquisitiones Arithmeticae
• 1802: Berechnung des jüdischen Osterfestes (Perhitungan Paskah Yahudi)
• 1804: Über die Grenzen der geocentrischen Oerter der Planeten (Tentang batas-batas tempat geosentris planet)
• 1808: Theorematis arithmetici demonstratio nova (Memperkenalkan lema Gauss, menggunakannya dalam bukti ketiga resiprositas kuadratik)
• 1808: Methodus peculiaris elevationem poli determinandi
• 1809: Theoria motus corporum coelestium in sectionibus conicis solem ambientium
• 1811: Disquisitio de elementis ellipticis Palladis ex oppositionibus annorum 1803, 1804, 1805, 1806, 1807, 1808, 1809 (Orbit Pallas)
• 1811: Summatio quarundam serierum singularium (Penentuan tanda jumlah Gauss kuadratik, menggunakannya untuk memberikan bukti keempat resiprositas kuadratik)
• 1813: Disquisitiones generales circa seriem infinitam 1+αβ/γ.1+etc. (berisi pecahan berlanjut Gauss)
• 1816: Demonstratio nova altera theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse
• 1816: Theorematis de resolubilitate functionum algebraicarum integrarum in factores reales demonstratio tertia
• 1816: Methodus nova integralium valores per approximationem inveniendi
• 1818: Theorematis fundamentalis in doctrina de residuis quadraticis demonstrationes et ampliationes novae (Bukti kelima dan keenam resiprositas kuadratik)
• 1818: Determinatio attractionis, quam in punctum positionis datae exerceret planeta, si eius massa per totamorbitam, ratione temporis, quo singulae partes describuntur, uniformiter esset dispertita (Hanya referensi ke - sebagian besar tidak diterbitkan - karya pada algoritma rata-rata aritmetika-geometris.)
• 1823: Theoria combinationis observationum erroribus minimis obnoxiae. Pars Prior
• 1823: Theoria combinationis observationum erroribus minimis obnoxiae. Pars Posterior
• 1825: Allgemeine Auflösung der Aufgabe die Theile einer gegebnen Fläche auf einer andern gegebnen Fläche so abzubilden dass die Abbildung dem Abgebildeten in den kleinsten Theilen ähnlich wird (Esai pemenang hadiah dari tahun 1822 tentang pemetaan konformal)
• 1828: Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona durch Beobachtungen am Ramsdenschen Zenithsector (Penentuan Perbedaan Lintang antara Observatorium Göttingen dan Altona dengan Observasi Sektor Zenit Ramsden)
• 1828: Supplementum theoriae combinationis observationum erroribus minimis obnoxiae
• 1828: Disquisitiones generales circa superficies curvas
• 1828: Theoria residuorum biquadraticorum, Commentatio prima
• 1832: Theoria residuorum biquadraticorum, Commentatio secunda (Memperkenalkan bilangan bulat Gauss, menyatakan (tanpa bukti) hukum resiprositas bikudratik, membuktikan hukum tambahan untuk 1 + i)
• 1845: Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung
• 1847: Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung
• 1848: Schreiben des Herrn Geheimen Hofrathes Gauss an den Herausgeber (Surat dari Tuan Penasihat Rahasia Pengadilan Gauss kepada editor)
• 1903: Wissenschaftliches Tagebuch (Buku Harian Ilmiah)

4.2. Fisika

• 1804: Fundamentalgleichungen für die Bewegung schwerer Körper auf der Erde (Persamaan fundamental untuk gerakan benda berat di Bumi)
• 1813: Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata (berisi teorema Gauss analisis vektor)
• 1817: Ueber die achromatischen Doppelobjective besonders in Rücksicht der vollkommnern Aufhebung der Farbenzerstreuung (Tentang lensa ganda akromatik dengan perhatian khusus pada dispersi warna yang lebih lengkap)
• 1829: Über ein neues allgemeines Grundgesetz der Mechanik (Tentang Hukum Fundamental Umum Mekanika yang baru)
• 1830: Principia generalia theoriae figurae fluidorum in statu aequilibrii
• 1836: Erdmagnetismus und Magnetometer (Geomagnetisme dan Magnetometer)
• 1840: Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnis des Quadrats der Entfernung wirkenden Anziehungs- und Abstoßungskräfte (Teorema Umum mengenai Gaya Tarik dan Tolak yang bekerja dalam Proporsi timbal balik dari Jarak kuadrat)
• 1841: Intensitas vis magneticae terrestris ad mensuram absolutam revocata (Intensitas Gaya Magnet Bumi Direduksi ke Pengukuran Absolut)
• 1843: Dioptrische Untersuchungen (Investigasi Dioptrik)

Bersama Wilhelm Weber:

• 1837-1839: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1836-1838
• 1840-1843: Resultate aus den Beobachtungen des magnetischen Vereins im Jahre 1839-1841
• 1840: Atlas des Erdmagnetismus nach den Elementen der Theorie entworfen. Supplement zu den Resultaten aus den Beobachtungen des magnetischen Vereins

4.3. Korespondensi

Korespondensi Gauss dengan para ilmuwan sezaman sangat penting karena memberikan wawasan tentang proses pemikirannya dan perkembangan ide-idenya. Koleksi lengkap surat-surat yang diketahui dari dan kepada Carl Friedrich Gauss tersedia secara daring melalui Akademi Ilmu Pengetahuan Göttingen. Warisan sastranya disimpan dan disediakan oleh Perpustakaan Negara dan Universitas Göttingen. Materi tertulis dari Carl Friedrich Gauss dan anggota keluarga juga dapat ditemukan di arsip kota Brunswick.

Beberapa korespondensi penting yang diterbitkan antara lain:

• Korespondensi antara Gauss dan Bessel (Desember 1804 hingga Agustus 1844)
• Surat kepada Boguslawski (Februari 1835 hingga Januari 1848)
• Korespondensi antara Carl Friedrich Gauss dan Johann Elert Bode (Februari 1802 hingga Oktober 1826)
• Korespondensi antara Carl Friedrich Gauss dan Wolfgang Bolyai (September 1797 hingga Februari 1853)
• Korespondensi antara Carl Friedrich Gauss dan Johann Franz Encke (Juni 1810 hingga Juni 1854)
• Korespondensi antara Carl Friedrich Gauss dan Christian Ludwig Gerling (Juni 1810 hingga Juni 1854)
• Surat antara Alexander von Humboldt dan Gauss (Juli 1807 hingga Desember 1854)
• Korespondensi antara Carl Friedrich Gauss dan Karl Kreil (1835 hingga 1843)
• Korespondensi antara Carl Friedrich Gauss dan Carl Ludwig von Lecoq (Februari 1799 hingga September 1800)
• Korespondensi antara Carl Friedrich Gauss dan Nevil Maskelyne (1802-05)
• Korespondensi antara Wilhelm Olbers dan Gauss (Januari 1802 hingga Mei 1839)
• Korespondensi antara C. F. Gauss dan H. C. Schumacher (April 1808 hingga November 1850)
• Korespondensi antara Carl Friedrich Gauss dan Eberhard August Zimmermann (1795 hingga 1815)