Archimedes

2.1. Kehidupan Awal

Archimedes lahir sekitar tahun 287 SM di kota pelabuhan Sirakusa, Sisilia, yang pada masa itu merupakan koloni otonom di Magna Graecia. Tanggal lahir ini didasarkan pada pernyataan sejarawan Yunani Bizantium, John Tzetzes, yang menyebutkan bahwa Archimedes hidup selama 75 tahun sebelum kematiannya pada tahun 212 SM. Dalam karyanya Perhitungan Pasir, Archimedes menyebutkan nama ayahnya adalah Phidias, seorang astronom yang tidak banyak diketahui detail lainnya.

Plutarch menulis dalam Kehidupan Paralel bahwa Archimedes memiliki hubungan kekerabatan dengan Raja Hiero II, penguasa Sirakusa. Namun, Cicero menyiratkan bahwa Archimedes berasal dari keluarga sederhana. Biografi Archimedes juga pernah ditulis oleh temannya, Heracleides, tetapi karya ini telah hilang, meninggalkan banyak detail kehidupannya yang tidak jelas. Misalnya, tidak diketahui apakah ia pernah menikah atau memiliki anak.

Meskipun demikian, dari karya-karya tulisnya yang masih bertahan, jelas bahwa ia menjalin hubungan kolegial dengan para sarjana di Alexandria, termasuk temannya Conon dari Samos dan kepala pustakawan Eratosthenes dari Kirene. Dalam kata pengantar Tentang Spiral yang ditujukan kepada Dositheus dari Pelusium, Archimedes menyebutkan bahwa "bertahun-tahun telah berlalu sejak kematian Conon," mengisyaratkan bahwa Archimedes mungkin sudah berusia lanjut saat menulis beberapa karyanya.

2.2. Karier

Versi standar kehidupan Archimedes ditulis lama setelah kematiannya oleh sejarawan Yunani dan Romawi. Referensi paling awal tentang Archimedes muncul dalam Sejarah karya Polybius (sekitar 200-118 SM), yang ditulis sekitar 70 tahun setelah kematiannya. Karya ini memberikan sedikit informasi tentang Archimedes sebagai pribadi, dan lebih banyak berfokus pada mesin perang yang ia bangun untuk mempertahankan Sirakusa dari Romawi.

Polybius mencatat bagaimana, selama Perang Punisia Kedua, Sirakusa mengubah kesetiaannya dari Roma ke Kartago, yang mengakibatkan kampanye militer di bawah komando Marcus Claudius Marcellus dan Appius Claudius Pulcher, yang mengepung kota dari tahun 213 hingga 212 SM. Ia mencatat bahwa Romawi meremehkan pertahanan Sirakusa, dan menyebutkan beberapa mesin yang dirancang Archimedes, termasuk katapel yang ditingkatkan, mesin mirip derek yang dapat diayunkan dalam busur, dan pelontar batu lainnya. Meskipun Romawi akhirnya merebut kota, mereka menderita kerugian besar karena kecerdikan Archimedes.

Cicero (106-43 SM) menyebut Archimedes dalam beberapa karyanya. Saat menjabat sebagai quaestor di Sisilia, Cicero menemukan apa yang diduga sebagai makam Archimedes di dekat gerbang Agrigentine di Sirakusa, dalam kondisi terbengkalai dan ditumbuhi semak-semak. Cicero membersihkan makam itu dan dapat melihat ukiran serta membaca beberapa bait yang telah ditambahkan sebagai prasasti. Makam itu dihiasi patung yang menggambarkan bukti matematika favorit Archimedes, yaitu bahwa volume dan luas permukaan bola adalah dua pertiga dari silinder yang melingkupinya, termasuk alasnya. Cicero juga menyebutkan bahwa Marcellus membawa ke Roma dua planetarium yang dibangun Archimedes. Sejarawan Romawi Livy (59 SM-17 M) menceritakan kembali kisah Polybius tentang penaklukan Sirakusa dan peran Archimedes di dalamnya.

2.3. Kematian

Archimedes meninggal selama pengepungan Sirakusa, ketika ia dibunuh oleh seorang prajurit Romawi meskipun ada perintah bahwa ia tidak boleh dilukai. Plutarch (45-119 M) memberikan setidaknya dua versi tentang bagaimana Archimedes meninggal setelah Sirakusa direbut. Menurut versi yang paling populer, Archimedes sedang merenungkan diagram matematika ketika kota itu direbut. Seorang prajurit Romawi memerintahkannya untuk datang dan bertemu Marcellus, tetapi ia menolak, mengatakan bahwa ia harus menyelesaikan masalah tersebut. Ini membuat prajurit itu marah, yang kemudian membunuh Archimedes dengan pedangnya.

Kisah lain menyebutkan Archimedes membawa instrumen matematika sebelum ia dibunuh karena seorang prajurit mengira itu adalah barang berharga. Marcellus dilaporkan marah atas kematian Archimedes, karena ia menganggapnya sebagai aset ilmiah yang berharga (ia menyebut Archimedes "Briareus geometris") dan telah memerintahkan agar ia tidak dilukai.

Kata-kata terakhir yang dikaitkan dengan Archimedes adalah "Jangan ganggu lingkaran saya" (Noli turbare circulos meos^{Bahasa Latin}; μὴ μου τοὺς κύκλους τάραττε^{Bahasa Yunani}), sebuah referensi ke gambar matematika yang konon sedang ia pelajari ketika diganggu oleh prajurit Romawi. Tidak ada bukti yang dapat diandalkan bahwa Archimedes mengucapkan kata-kata ini dan tidak muncul dalam catatan Plutarch. Kutipan serupa ditemukan dalam karya Valerius Maximus (sekitar 30 M), yang menulis dalam Perbuatan dan Ucapan yang Berkesan, "... sed protecto manibus puluere 'noli' inquit, 'obsecro, istum disturbare'^{Bahasa Latin}" ("... tetapi melindungi debu dengan tangannya, berkata 'Saya mohon, jangan ganggu ini'").

Makam Archimedes, yang di atasnya terdapat bola dan silinder, ditemukan oleh Cicero pada tahun 75 SM, 137 tahun setelah kematian Archimedes. Cicero saat itu menjabat sebagai quaestor di Sisilia. Ia mendengar cerita tentang makam Archimedes dan setelah mencari-cari, ia menemukannya di dekat gerbang Agrigentine di Sirakusa, dalam kondisi terbengkalai dan ditumbuhi semak belukar. Cicero membersihkan makam itu dan dapat melihat ukiran serta membaca beberapa bait yang telah ditambahkan sebagai prasasti. Ukiran tersebut menggambarkan bukti matematika favorit Archimedes, yaitu bahwa volume dan luas permukaan bola adalah dua pertiga dari silinder yang melingkupinya, termasuk alasnya.

3.1. Metode Penghabisan dan Infinitesimal

Archimedes mampu menggunakan indivisibel (pendahulu infinitesimal) dengan cara yang mirip dengan kalkulus integral modern. Melalui bukti dengan kontradiksi (reductio ad absurdum), ia dapat memberikan jawaban untuk masalah hingga tingkat akurasi arbitrer, sambil menentukan batas-batas di mana jawaban itu berada. Teknik ini dikenal sebagai metode penghabisan, dan ia menggunakannya untuk memperkirakan luas bangun dan nilai pi (π).

3.2. Perkiraan Pi

Dalam Pengukuran Lingkaran, Archimedes menghitung nilai pi (π) dengan menggambar segi enam beraturan yang lebih besar di luar lingkaran dan kemudian segi enam beraturan yang lebih kecil di dalam lingkaran. Ia secara progresif menggandakan jumlah sisi setiap poligon beraturan, menghitung panjang sisi setiap poligon pada setiap langkah. Seiring bertambahnya jumlah sisi, poligon menjadi perkiraan lingkaran yang lebih akurat. Setelah empat langkah tersebut, ketika poligon masing-masing memiliki 96 sisi, ia dapat menentukan bahwa nilai π berada antara 3 1/7 (sekitar 3.1429) dan 3 10/71 (sekitar 3.1408), yang konsisten dengan nilai sebenarnya sekitar 3.1416. Ia juga membuktikan bahwa luas lingkaran sama dengan π dikalikan dengan kuadrat jari-jari lingkaran (πr²).

3.3. Geometri

Archimedes adalah seorang ahli geometri yang ulung. Ia menurunkan rumus-rumus untuk luas lingkaran, luas permukaan dan volume bola, serta luas di bawah parabola, dan bentuk geometris lainnya yang mendalam. Dalam Tentang Bola dan Silinder, ia memperoleh hasil yang paling ia banggakan, yaitu hubungan antara bola dan silinder yang melingkupinya dengan tinggi dan diameter yang sama. Volume bola adalah 4/3πr³, dan untuk silinder adalah 2πr³. Luas permukaan bola adalah 4πr², dan luas permukaan silinder adalah 6πr² (termasuk kedua alasnya), di mana r adalah jari-jari bola dan silinder. Hasil ini menunjukkan bahwa volume dan luas permukaan bola selalu dua pertiga dari silinder yang melingkupinya.

Dalam Kuadratur Parabola, Archimedes membuktikan bahwa luas yang dilingkupi oleh parabola dan garis lurus adalah 4/3 kali luas segitiga yang sesuai yang diinskripsikan, seperti yang ditunjukkan pada gambar di samping. Ia menyatakan solusi masalah ini sebagai deret geometri tak hingga dengan rasio umum 1/4:


Jika suku pertama dalam deret ini adalah luas segitiga, maka suku kedua adalah jumlah luas dua segitiga yang alasnya adalah dua garis sekan yang lebih kecil, dan seterusnya. Bukti ini menggunakan variasi deret 1/4 + 1/16 + 1/64 + 1/256 + ... yang berjumlah 1/3.

3.4. Sifat Archimedean

Dalam Tentang Bola dan Silinder, Archimedes mengemukakan postulat bahwa setiap besaran, jika ditambahkan pada dirinya sendiri berkali-kali, akan melebihi besaran yang diberikan. Hari ini ini dikenal sebagai Sifat Archimedean dari bilangan real.

Archimedes memberikan nilai akar kuadrat dari 3 yang terletak antara 265/153 (sekitar 1.7320261) dan 1351/780 (sekitar 1.7320512) dalam Pengukuran Lingkaran. Nilai sebenarnya adalah sekitar 1.7320508, menjadikan ini perkiraan yang sangat akurat. Ia memperkenalkan hasil ini tanpa memberikan penjelasan tentang bagaimana ia memperolehnya. Aspek karya Archimedes ini menyebabkan John Wallis berkomentar bahwa ia: "seolah-olah dengan sengaja menutupi jejak penyelidikannya seolah-olah ia iri pada generasi mendatang rahasia metode penyelidikannya sementara ia ingin memeras persetujuan dari mereka untuk hasil-hasilnya." Ada kemungkinan bahwa ia menggunakan prosedur iterasi untuk menghitung nilai-nilai ini.

3.5. Perhitungan Pasir

Dalam Perhitungan Pasir, Archimedes berupaya menghitung jumlah yang lebih besar dari butiran pasir yang dibutuhkan untuk mengisi alam semesta. Dengan demikian, ia menantang gagasan bahwa jumlah butiran pasir terlalu besar untuk dihitung. Ia menulis:
"Ada beberapa, Raja Gelo, yang berpikir bahwa jumlah pasir itu tak terbatas; dan yang saya maksud dengan pasir bukan hanya yang ada di sekitar Sirakusa dan Sisilia lainnya tetapi juga yang ditemukan di setiap wilayah baik yang berpenghuni maupun tidak berpenghuni."
Untuk memecahkan masalah ini, Archimedes merancang sistem penghitungan berdasarkan miriad. Kata itu sendiri berasal dari bahasa Yunani μυριάς^{Bahasa Yunani Kuno}, untuk angka 10.000. Ia mengusulkan sistem angka menggunakan pangkat dari miriad miriad (100 juta, yaitu 10.000 x 10.000) dan menyimpulkan bahwa jumlah butiran pasir yang dibutuhkan untuk mengisi alam semesta adalah 8 vigintillion, atau 8×10⁶³.

3.6. Karya Utama (Matematika)

Archimedes menghasilkan sejumlah besar karya matematika yang mendalam, beberapa di antaranya masih bertahan hingga kini dan memberikan wawasan langsung ke dalam pemikirannya.

• Pengukuran Lingkaran

Ini adalah karya singkat yang terdiri dari tiga proposisi. Ini ditulis dalam bentuk korespondensi dengan Dositheus dari Pelusium, yang merupakan murid Conon dari Samos. Dalam Proposisi II, Archimedes memberikan perkiraan nilai pi (π), menunjukkan bahwa itu lebih besar dari 223/71 (3.1408...) dan kurang dari 22/7 (3.1428...).

• Kuadratur Parabola

Dalam karya 24 proposisi yang ditujukan kepada Dositheus ini, Archimedes membuktikan dengan dua metode bahwa luas yang dilingkupi oleh parabola dan garis lurus adalah 4/3 kali luas segitiga yang sesuai yang diinskripsikan, menggunakan deret geometri tak hingga.

• Tentang Bola dan Silinder

Risalah dua volume ini membahas hubungan antara bola dan silinder yang melingkupinya. Archimedes membuktikan bahwa volume dan luas permukaan bola adalah dua pertiga dari silinder yang melingkupinya, sebuah penemuan yang sangat ia banggakan.

• Tentang Spiral

Karya 28 proposisi ini juga ditujukan kepada Dositheus. Risalah ini mendefinisikan apa yang sekarang disebut spiral Archimedes, yaitu lokus titik yang bergerak menjauh dari titik tetap dengan kecepatan konstan sepanjang garis yang berputar dengan kecepatan sudut konstan. Secara ekuivalen, dalam sistem koordinat polar modern (r, θ), itu dapat dijelaskan dengan persamaan r=a+bθ dengan bilangan real a dan b. Ini adalah contoh awal dari kurva mekanis (kurva yang dilacak oleh titik yang bergerak) yang dipertimbangkan oleh seorang matematikawan Yunani.

• Tentang Konoid dan Sferoid

Ini adalah karya dalam 32 proposisi yang ditujukan kepada Dositheus. Dalam risalah ini Archimedes menghitung luas dan volume penampang kerucut, bola, dan paraboloid.

• Tentang Benda Mengapung

Karya ini membahas hukum kesetimbangan fluida dan prinsip daya apung, yang dikenal sebagai Prinsip Archimedes.

• Ostomachion

Juga dikenal sebagai Loculus Archimedes atau Kotak Archimedes, ini adalah teka-teki diseksi yang mirip dengan Tangram. Archimedes menghitung luas 14 bagian yang dapat dirakit untuk membentuk sebuah persegi.

• Masalah Sapi Archimedes

Sebuah masalah persamaan Diophantine yang menantang para matematikawan untuk menghitung jumlah sapi dalam kawanan Matahari. Solusinya adalah angka yang sangat besar, sekitar 7.760271×10²⁰⁶⁵⁴⁴.

• Perhitungan Pasir

Dalam risalah ini, Archimedes mengembangkan sistem penomoran untuk menyatakan bilangan yang sangat besar, menghitung jumlah butiran pasir yang dibutuhkan untuk mengisi alam semesta.

• Metode Teorema Mekanis

Risalah ini ditemukan kembali dalam Archimedes Palimpsest. Di dalamnya, Archimedes menggunakan indivisibel untuk menunjukkan bagaimana memecah suatu bangun menjadi bagian-bagian yang tak terhingga kecilnya dapat digunakan untuk menentukan luas atau volumenya. Ia mungkin menganggap metode ini kurang ketat secara formal, jadi ia juga menggunakan metode penghabisan untuk mendapatkan hasilnya.

4.1. Prinsip Archimedes

Anekdot yang paling dikenal tentang Archimedes menceritakan bagaimana ia menemukan metode untuk menentukan volume benda berbentuk tidak beraturan. Menurut Vitruvius, sebuah mahkota telah dibuat untuk Raja Hiero II dari Sirakusa, yang menyediakan emas murni untuk digunakan. Mahkota itu kemungkinan dibuat dalam bentuk karangan bunga votif. Archimedes diminta untuk menentukan apakah beberapa perak telah diganti oleh tukang emas tanpa merusak mahkota, sehingga ia tidak bisa melelehkannya menjadi benda berbentuk teratur untuk menghitung densitasnya.

Dalam kisah ini, Archimedes memperhatikan saat mandi bahwa permukaan air di bak naik saat ia masuk, dan menyadari bahwa efek ini dapat digunakan untuk menentukan volume mahkota emas. Archimedes begitu gembira dengan penemuan ini sehingga ia berlari ke jalan telanjang, lupa berpakaian, sambil berteriak "Eureka!" (εὕρηκα^{Bahasa Yunani}, heúrēka!, "Saya telah menemukannya!"). Untuk tujuan praktis, air tidak dapat dikompresi, sehingga mahkota yang terendam akan memindahkan sejumlah air yang sama dengan volumenya sendiri. Dengan membagi massa mahkota dengan volume air yang dipindahkan, densitasnya dapat diperoleh; jika logam yang lebih murah dan kurang padat telah ditambahkan, densitasnya akan lebih rendah daripada emas. Archimedes menemukan bahwa inilah yang terjadi, membuktikan bahwa perak telah dicampur.

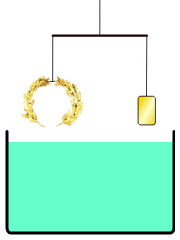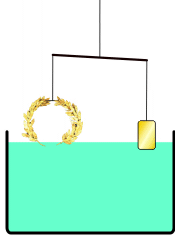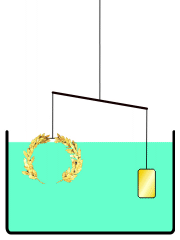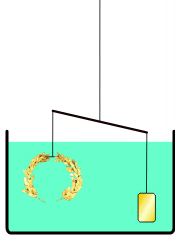
Kisah mahkota emas tidak muncul di mana pun dalam karya Archimedes yang diketahui. Kepraktisan metode yang dijelaskan telah dipertanyakan karena akurasi ekstrem yang diperlukan untuk mengukur perpindahan air. Archimedes mungkin malah mencari solusi yang menerapkan prinsip hidrostatika yang dikenal sebagai Prinsip Archimedes, yang ditemukan dalam risalahnya Tentang Benda Mengapung: sebuah benda yang terendam dalam fluida mengalami gaya apung yang sama dengan berat fluida yang dipindahkannya. Menggunakan prinsip ini, dimungkinkan untuk membandingkan densitas mahkota dengan emas murni dengan menimbangnya di timbangan dengan sampel emas murni dengan berat yang sama, kemudian merendam alat tersebut dalam air. Perbedaan densitas antara kedua sampel akan menyebabkan timbangan miring sesuai. Galileo Galilei, yang menemukan keseimbangan hidrostatik pada tahun 1586 yang terinspirasi oleh karya Archimedes, menganggapnya "kemungkinan metode ini sama dengan yang diikuti Archimedes, karena, selain sangat akurat, itu didasarkan pada demonstrasi yang ditemukan oleh Archimedes sendiri."

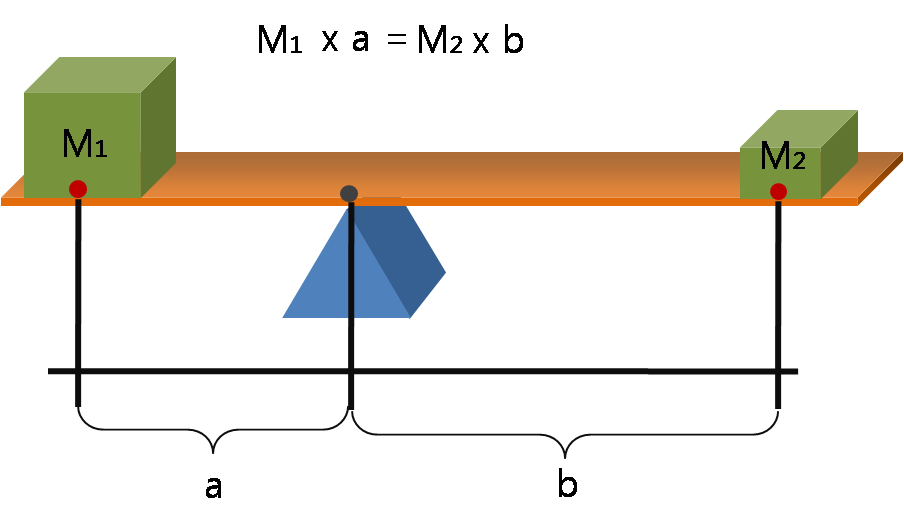
4.2. Hukum Tuas

Meskipun Archimedes tidak menemukan tuas, ia memberikan bukti matematis dari prinsip yang terlibat dalam karyanya Tentang Keseimbangan Bidang. Deskripsi awal prinsip tuas ditemukan dalam karya Euclid dan dalam Masalah Mekanis, milik Sekolah Peripatetik pengikut Aristoteles, yang kepengarangannya telah dikaitkan oleh beberapa orang dengan Archytas.

Ada beberapa laporan, yang sering bertentangan, mengenai prestasi Archimedes menggunakan tuas untuk mengangkat benda yang sangat berat. Plutarch menjelaskan bagaimana Archimedes merancang sistem katrol blok dan takel, memungkinkan para pelaut untuk menggunakan prinsip daya ungkit untuk mengangkat benda yang seharusnya terlalu berat untuk dipindahkan. Menurut Pappus dari Alexandria, karya Archimedes tentang tuas dan pemahamannya tentang keuntungan mekanis menyebabkannya berkomentar: "Berikan aku tempat untuk berdiri, dan aku akan memindahkan Bumi" (δῶς μοι πᾶ στῶ καὶ τὰν gân kineō^{Bahasa Yunani}). Olympiodorus Muda kemudian mengaitkan kebanggaan yang sama dengan penemuan baroulkos oleh Archimedes, sejenis kerek, daripada tuas.

4.3. Statika dan Hidrostatika

Archimedes memberikan kontribusi besar dalam bidang statika dan hidrostatika, yang menjadi fondasi fisika terapan. Karyanya Tentang Keseimbangan Bidang secara matematis membuktikan hukum tuas dan menjelaskan konsep pusat massa. Ia menerapkan prinsip-prinsip ini untuk menghitung luas dan pusat gravitasi berbagai bentuk geometris, termasuk segitiga, jajar genjang, dan parabola.

Dalam Tentang Benda Mengapung, ia menguraikan hukum kesetimbangan fluida dan membuktikan bahwa air akan berbentuk bola di sekitar pusat gravitasi. Ini mungkin merupakan upaya untuk menjelaskan teori astronom Yunani kontemporer seperti Eratosthenes bahwa Bumi itu bulat. Fluida yang dijelaskan oleh Archimedes tidak mandiri, karena ia mengasumsikan keberadaan titik di mana segala sesuatu jatuh untuk mendapatkan bentuk bola. Prinsip Archimedes tentang daya apung, yang menyatakan bahwa "setiap benda yang seluruhnya atau sebagian terendam dalam fluida mengalami gaya dorong ke atas yang sama dengan, tetapi berlawanan arah dengan, berat fluida yang dipindahkan," juga diberikan dalam karya ini.

4.4. Penemuan dan Invensi

Archimedes dikenal karena merancang berbagai mesin inovatif yang menunjukkan kecerdasan praktis dan inovatifnya, terutama untuk memenuhi kebutuhan kota asalnya, Sirakusa.

4.4.1. Pompa Ulir (Ulir Archimedes)

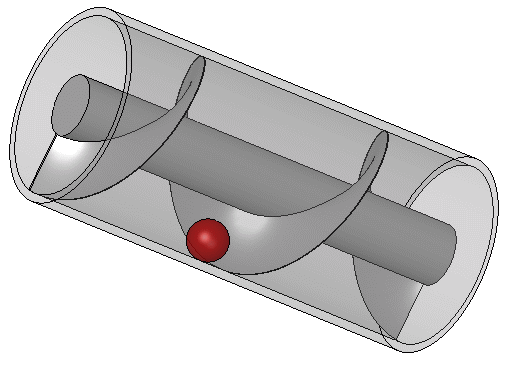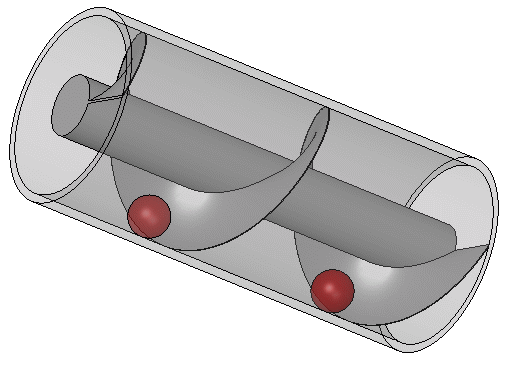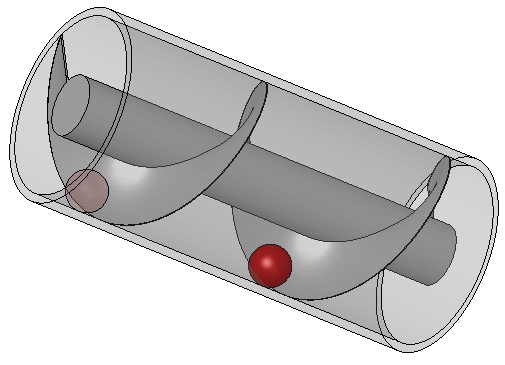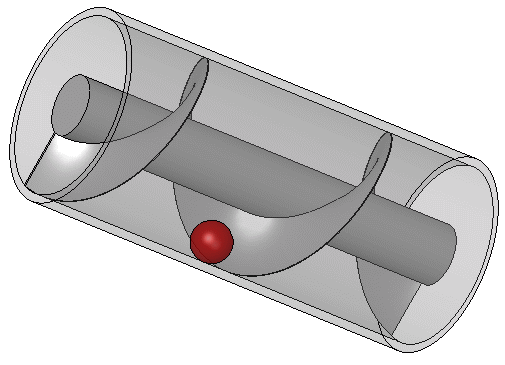
Sebagian besar karya Archimedes dalam bidang teknik kemungkinan besar muncul dari pemenuhan kebutuhan kota asalnya, Sirakusa. Athenaeus dari Naukratis mengutip seorang Moschion dalam deskripsi tentang bagaimana Raja Hiero II menugaskan desain sebuah kapal besar, Syracusia, yang dapat digunakan untuk perjalanan mewah, mengangkut persediaan, dan sebagai tampilan kekuatan angkatan laut. Syracusia dikatakan sebagai kapal terbesar yang dibangun di zaman klasik dan, menurut catatan Moschion, diluncurkan oleh Archimedes. Kapal itu konon mampu mengangkut 600 orang dan termasuk dekorasi taman, gimnasium, dan kuil yang didedikasikan untuk dewi Afrodit di antara fasilitasnya. Catatan itu juga menyebutkan bahwa, untuk menghilangkan air yang mungkin bocor melalui lambung, sebuah alat dengan bilah berbentuk ulir yang berputar di dalam silinder dirancang oleh Archimedes.

Ulir Archimedes diputar dengan tangan, dan juga dapat digunakan untuk memindahkan air dari badan air yang rendah ke saluran irigasi. Ulir ini masih digunakan hingga kini untuk memompa cairan dan padatan butiran seperti batu bara dan biji-bijian. Dijelaskan oleh Vitruvius, alat Archimedes mungkin merupakan peningkatan dari pompa ulir yang digunakan untuk mengairi Taman Gantung Babel. Kapal uap SS Archimedes yang pertama berlayar dengan baling-baling ulir diluncurkan pada tahun 1839 dan dinamai untuk menghormati Archimedes dan karyanya pada ulir.

4.4.4. Penemuan Lainnya

Archimedes juga dikreditkan dengan penemuan odometer selama Perang Punisia Pertama. Odometer digambarkan sebagai gerobak dengan mekanisme roda gigi yang menjatuhkan bola ke dalam wadah setelah setiap mil perjalanan.

Sebagai legenda, Archimedes mengatur cermin sebagai reflektor parabola untuk membakar kapal yang menyerang Sirakusa menggunakan sinar matahari yang terfokus. Meskipun tidak ada bukti kontemporer yang masih ada tentang prestasi ini dan para sarjana modern percaya itu tidak terjadi, Archimedes mungkin telah menulis sebuah karya tentang cermin berjudul Catoptrica. Lucian dan Galen, yang menulis pada abad kedua Masehi, menyebutkan bahwa selama pengepungan Sirakusa Archimedes telah membakar kapal musuh. Hampir empat ratus tahun kemudian, Anthemius dari Tralles, meskipun skeptis, mencoba merekonstruksi geometri reflektor hipotetis Archimedes.

Perangkat yang diduga, kadang-kadang disebut "Sinar panas Archimedes", telah menjadi subjek perdebatan yang sedang berlangsung tentang kredibilitasnya sejak Renaisans. René Descartes menolaknya sebagai palsu, sementara para peneliti modern telah mencoba menciptakan kembali efek tersebut hanya dengan sarana yang akan tersedia bagi Archimedes, sebagian besar dengan hasil negatif. Telah disarankan bahwa susunan besar perisai perunggu atau tembaga yang sangat dipoles yang berfungsi sebagai cermin bisa digunakan untuk memfokuskan sinar matahari ke kapal, tetapi efek keseluruhannya akan membutakan, menyilaukan, atau mengganggu kru kapal daripada membakar. Menggunakan bahan modern dan skala yang lebih besar, tungku surya yang memusatkan sinar matahari dapat mencapai suhu yang sangat tinggi, dan kadang-kadang digunakan untuk menghasilkan listrik.

5.1. Karya yang Bertahan

Berikut adalah karya-karya Archimedes yang masih bertahan, diurutkan secara kronologis berdasarkan kriteria terminologi dan sejarah baru yang ditetapkan oleh Knorr (1978) dan Sato (1986).

• Pengukuran Lingkaran

Ini adalah karya singkat yang terdiri dari tiga proposisi. Ini ditulis dalam bentuk korespondensi dengan Dositheus dari Pelusium, yang merupakan murid Conon dari Samos. Dalam Proposisi II, Archimedes memberikan perkiraan nilai pi (π), menunjukkan bahwa itu lebih besar dari 223/71 (3.1408...) dan kurang dari 22/7 (3.1428...).

• Perhitungan Pasir

Dalam risalah ini, juga dikenal sebagai Psammites, Archimedes menemukan angka yang lebih besar dari butiran pasir yang dibutuhkan untuk mengisi alam semesta. Buku ini menyebutkan teori heliosentris tata surya yang diusulkan oleh Aristarchus dari Samos, serta ide-ide kontemporer tentang ukuran Bumi dan jarak antara berbagai benda langit, dan upaya untuk mengukur diameter semu Matahari. Dengan menggunakan sistem angka berdasarkan pangkat miriad, Archimedes menyimpulkan bahwa jumlah butiran pasir yang dibutuhkan untuk mengisi alam semesta adalah 8×10⁶³ dalam notasi modern. Surat pengantar menyatakan bahwa ayah Archimedes adalah seorang astronom bernama Phidias. Perhitungan Pasir adalah satu-satunya karya yang bertahan di mana Archimedes membahas pandangannya tentang astronomi.

• Tentang Keseimbangan Bidang

Ada dua buku dalam Tentang Keseimbangan Bidang: yang pertama berisi tujuh aksioma dan lima belas proposisi, sedangkan buku kedua berisi sepuluh proposisi. Dalam buku pertama, Archimedes membuktikan hukum tuas, yang menyatakan bahwa: "Besaran berada dalam keseimbangan pada jarak yang berbanding terbalik dengan beratnya." Archimedes menggunakan prinsip-prinsip yang diturunkan untuk menghitung luas dan pusat massa berbagai bentuk geometris termasuk segitiga, jajar genjang, dan parabola.

• Kuadratur Parabola

Dalam karya 24 proposisi yang ditujukan kepada Dositheus ini, Archimedes membuktikan dengan dua metode bahwa luas yang dilingkupi oleh parabola dan garis lurus adalah 4/3 kali luas segitiga yang diinskripsikan yang sesuai seperti yang ditunjukkan pada gambar di samping. Ia mencapai ini dalam salah satu buktinya dengan menghitung nilai deret geometri yang berjumlah tak hingga dengan rasio 1/4.

• Tentang Bola dan Silinder

Dalam risalah dua volume yang ditujukan kepada Dositheus ini, Archimedes memperoleh hasil yang paling ia banggakan, yaitu hubungan antara bola dan silinder yang melingkupinya dengan tinggi dan diameter yang sama. Volume bola adalah 4/3πr³, dan untuk silinder adalah 2πr³. Luas permukaan bola adalah 4πr², dan luas permukaan silinder adalah 6πr² (termasuk kedua alasnya), di mana r adalah jari-jari bola dan silinder.

• Tentang Spiral

Karya 28 proposisi ini juga ditujukan kepada Dositheus. Risalah ini mendefinisikan apa yang sekarang disebut spiral Archimedes, yaitu lokus titik yang bergerak menjauh dari titik tetap dengan kecepatan konstan sepanjang garis yang berputar dengan kecepatan sudut konstan. Secara ekuivalen, dalam sistem koordinat polar modern (r, θ), itu dapat dijelaskan dengan persamaan r=a+bθ dengan bilangan real a dan b. Ini adalah contoh awal dari kurva mekanis (kurva yang dilacak oleh titik yang bergerak) yang dipertimbangkan oleh seorang matematikawan Yunani.

• Tentang Konoid dan Sferoid

Ini adalah karya dalam 32 proposisi yang ditujukan kepada Dositheus. Dalam risalah ini Archimedes menghitung luas dan volume penampang kerucut, bola, dan paraboloid.

• Tentang Benda Mengapung

Ada dua buku Tentang Benda Mengapung. Dalam buku pertama, Archimedes menjelaskan hukum keseimbangan fluida dan membuktikan bahwa air akan berbentuk bola di sekitar pusat gravitasi. Ini mungkin merupakan upaya untuk menjelaskan teori astronom Yunani kontemporer seperti Eratosthenes bahwa Bumi itu bulat. Fluida yang dijelaskan oleh Archimedes tidak mandiri, karena ia mengasumsikan keberadaan titik di mana segala sesuatu jatuh untuk mendapatkan bentuk bola. Prinsip Archimedes tentang daya apung diberikan dalam karya ini, yang dinyatakan sebagai berikut: "Setiap benda yang seluruhnya atau sebagian terendam dalam fluida mengalami gaya dorong ke atas yang sama dengan, tetapi berlawanan arah dengan, berat fluida yang dipindahkan." Dalam bagian kedua, ia menghitung posisi keseimbangan bagian-bagian paraboloid. Ini mungkin merupakan idealisasi bentuk lambung kapal. Beberapa bagiannya mengapung dengan alas di bawah air dan puncaknya di atas air, mirip dengan cara gunung es mengapung.

• Ostomachion

Juga dikenal sebagai Loculus Archimedes atau Kotak Archimedes, ini adalah teka-teki diseksi yang mirip dengan Tangram, dan risalah yang menggambarkannya ditemukan dalam bentuk yang lebih lengkap di Archimedes Palimpsest. Archimedes menghitung luas 14 bagian yang dapat dirakit untuk membentuk sebuah persegi. Reviel Netz dari Universitas Stanford berpendapat pada tahun 2003 bahwa Archimedes berusaha menentukan berapa banyak cara bagian-bagian itu dapat dirakit menjadi bentuk persegi. Netz menghitung bahwa bagian-bagian itu dapat dibuat menjadi persegi dalam 17.152 cara. Jumlah susunan adalah 536 ketika solusi yang setara dengan rotasi dan refleksi dikecualikan. Teka-teki ini merupakan contoh masalah awal dalam kombinatorika. Asal usul nama teka-teki itu tidak jelas, dan telah disarankan bahwa itu diambil dari kata bahasa Yunani Kuno untuk "tenggorokan" atau "kerongkongan", stomachos (στόμαχος^{Bahasa Yunani Kuno}). Ausonius menyebut teka-teki itu Ostomachion, sebuah kata majemuk Yunani yang dibentuk dari akar kata osteon^{Bahasa Yunani Kuno} (ὀστέον^{Bahasa Yunani Kuno}, lit. "tulang") dan machē^{Bahasa Yunani Kuno} (μάχη^{Bahasa Yunani Kuno}, lit. "perkelahian").

• Masalah Sapi Archimedes

Gotthold Ephraim Lessing menemukan karya ini dalam manuskrip Yunani yang terdiri dari puisi 44 baris di Perpustakaan Herzog August di Wolfenbüttel, Jerman pada tahun 1773. Ini ditujukan kepada Eratosthenes dan para matematikawan di Alexandria. Archimedes menantang mereka untuk menghitung jumlah sapi di Kawanan Helios dengan memecahkan sejumlah persamaan Diophantine simultan. Ada versi masalah yang lebih sulit di mana beberapa jawaban harus berupa bilangan kuadrat. A. Amthor pertama kali memecahkan versi masalah ini pada tahun 1880, dan jawabannya adalah bilangan yang sangat besar, sekitar 7.760271×10²⁰⁶⁵⁴⁴.

• Perhitungan Pasir

Dalam risalah ini, Archimedes mengembangkan sistem penomoran untuk menyatakan bilangan yang sangat besar, menghitung jumlah butiran pasir yang dibutuhkan untuk mengisi alam semesta.

• Metode Teorema Mekanis

Risalah ini dianggap hilang sampai penemuan Archimedes Palimpsest pada tahun 1906. Dalam karya ini Archimedes menggunakan indivisibel, dan menunjukkan bagaimana memecah suatu bangun menjadi sejumlah tak terbatas bagian-bagian yang tak terhingga kecilnya dapat digunakan untuk menentukan luas atau volumenya. Ia mungkin menganggap metode ini kurang ketat secara formal, jadi ia juga menggunakan metode penghabisan untuk mendapatkan hasilnya.

5.2. Karya yang Hilang

Beberapa karya Archimedes hanya diketahui melalui referensi dari penulis kuno lainnya, menunjukkan luasnya kontribusi yang mungkin telah hilang. Ini termasuk Tentang Pembuatan Bola dan karya tentang polihedra yang disebutkan oleh Pappus dari Alexandria; Catoptrica, sebuah karya tentang optik yang disebutkan oleh Theon dari Alexandria; Prinsip, yang ditujukan kepada Zeuxippus dan menjelaskan sistem bilangan yang digunakan dalam Perhitungan Pasir; Tentang Timbangan atau Tentang Tuas; Tentang Pusat Gravitasi; dan Tentang Kalender.

Karya apokrifa lainnya termasuk Buku Lemma atau Liber Assumptorum, sebuah risalah dengan 15 proposisi tentang sifat lingkaran. Salinan teks tertua yang diketahui adalah dalam bahasa Arab. T. L. Heath dan Marshall Clagett berpendapat bahwa itu tidak mungkin ditulis oleh Archimedes dalam bentuknya saat ini, karena mengutip Archimedes, menunjukkan modifikasi oleh penulis lain. Lemma mungkin didasarkan pada karya Archimedes sebelumnya yang sekarang hilang.

Juga diklaim bahwa rumus Heron untuk menghitung luas segitiga dari panjang sisinya diketahui oleh Archimedes, meskipun kemunculan pertamanya adalah dalam karya Hero dari Alexandria pada abad ke-1 M. Atribusi lain yang dipertanyakan pada karya Archimedes termasuk puisi Latin Carmen de ponderibus et mensuris (abad ke-4 atau ke-5), yang menggambarkan penggunaan keseimbangan hidrostatik untuk memecahkan masalah mahkota, dan teks abad ke-12 Mappae clavicula, yang berisi instruksi tentang cara melakukan pengujian logam dengan menghitung berat jenisnya.

5.3. Archimedes Palimpsest

Dokumen terpenting yang berisi karya Archimedes adalah Archimedes Palimpsest. Pada tahun 1906, profesor Denmark Johan Ludvig Heiberg mengunjungi Konstantinopel untuk memeriksa perkamen kulit kambing setebal 174 halaman berisi doa-doa, yang ditulis pada abad ke-13, setelah membaca transkripsi singkat yang diterbitkan tujuh tahun sebelumnya oleh Papadopoulos-Kerameus. Ia memastikan bahwa itu memang sebuah palimpsest, sebuah dokumen dengan teks yang telah ditulis di atas karya lama yang terhapus. Palimpsest dibuat dengan mengikis tinta dari karya yang ada dan menggunakannya kembali, praktik umum di Abad Pertengahan, karena vellum mahal. Karya-karya lama dalam palimpsest diidentifikasi oleh para sarjana sebagai salinan risalah Archimedes yang sebelumnya hilang dari abad ke-10. Perkamen itu menghabiskan ratusan tahun di perpustakaan biara di Konstantinopel sebelum dijual kepada kolektor pribadi pada tahun 1920-an. Pada 29 Oktober 1998, itu dijual di lelang kepada pembeli anonim dengan total 2.20 M USD.

Palimpsest ini menyimpan tujuh risalah, termasuk satu-satunya salinan Tentang Benda Mengapung yang masih ada dalam bahasa Yunani asli. Ini adalah satu-satunya sumber yang diketahui dari Metode Teorema Mekanis, yang disebut oleh Suda dan dianggap telah hilang selamanya. Ostomachion juga ditemukan dalam palimpsest, dengan analisis teka-teki yang lebih lengkap daripada yang ditemukan dalam teks-teks sebelumnya. Palimpsest itu disimpan di Museum Seni Walters di Baltimore, Maryland, di mana ia menjalani berbagai tes modern termasuk penggunaan ultraviolet dan sinar-X untuk membaca teks yang ditimpa. Sejak itu ia kembali ke pemilik anonimnya.

Risalah-risalah dalam Archimedes Palimpsest meliputi:

• Tentang Keseimbangan Bidang
• Tentang Spiral
• Pengukuran Lingkaran
• Tentang Bola dan Silinder
• Tentang Benda Mengapung
• Metode Teorema Mekanis
• Ostomachion
• Pidato oleh politikus abad ke-4 SM Hypereides
• Komentar tentang Kategori Aristoteles
• Karya-karya lainnya

6.1. Pengaruh pada Matematika dan Fisika

Sejarawan sains dan matematika hampir secara universal setuju bahwa Archimedes adalah matematikawan terbaik dari zaman kuno. Eric Temple Bell, misalnya, menulis: "Daftar tiga matematikawan 'terbesar' sepanjang sejarah akan mencakup nama Archimedes. Dua lainnya yang biasanya dikaitkan dengannya adalah Isaac Newton dan Carl Friedrich Gauss. Beberapa, mempertimbangkan kekayaan relatif-atau kemiskinan-matematika dan ilmu fisika di zaman masing-masing di mana para raksasa ini hidup, dan memperkirakan pencapaian mereka dengan latar belakang zaman mereka, akan menempatkan Archimedes pertama."

Demikian pula, Alfred North Whitehead dan George F. Simmons berkata tentang Archimedes: "... pada tahun 1500 Eropa tahu lebih sedikit daripada Archimedes yang meninggal pada tahun 212 SM ..." dan "Jika kita mempertimbangkan apa yang dicapai semua orang lain dalam matematika dan fisika, di setiap benua dan di setiap peradaban, dari awal waktu hingga abad ketujuh belas di Eropa Barat, pencapaian Archimedes mengalahkan semuanya. Dia adalah peradaban besar sendirian."

Reviel Netz, Profesor Suppes dalam Matematika dan Astronomi Yunani di Universitas Stanford dan seorang ahli Archimedes mencatat: "Dan demikian, karena Archimedes memimpin lebih dari siapa pun dalam pembentukan kalkulus dan karena ia adalah pelopor penerapan matematika ke dunia fisik, ternyata sains Barat hanyalah serangkaian catatan kaki untuk Archimedes. Dengan demikian, ternyata Archimedes adalah ilmuwan terpenting yang pernah hidup."

Leonardo da Vinci berulang kali menyatakan kekagumannya pada Archimedes, dan mengaitkan penemuannya Architonnerre dengan Archimedes. Galileo Galilei menyebutnya "manusia super" dan "guruku", sementara Christiaan Huygens berkata, "Saya pikir Archimedes tidak sebanding dengan siapa pun," secara sadar menirunya dalam karya awalnya. Gottfried Wilhelm Leibniz berkata, "Siapa pun yang memahami Archimedes dan Apollonius dari Perga akan kurang mengagumi pencapaian orang-orang terkemuka di kemudian hari." Pahlawan Gauss adalah Archimedes dan Newton, dan Moritz Cantor, yang belajar di bawah Gauss di Universitas Göttingen, melaporkan bahwa ia pernah berkomentar dalam percakapan bahwa "hanya ada tiga matematikawan yang membuat zaman: Archimedes, Newton, dan Eisenstein."

Penemu Nikola Tesla memujinya, dengan mengatakan: "Archimedes adalah idola saya. Saya mengagumi karya-karya seniman, tetapi menurut saya, mereka hanyalah bayangan dan kemiripan. Penemu, saya pikir, memberikan kepada dunia ciptaan yang nyata, yang hidup dan bekerja."

6.2. Penghormatan dan Peringatan

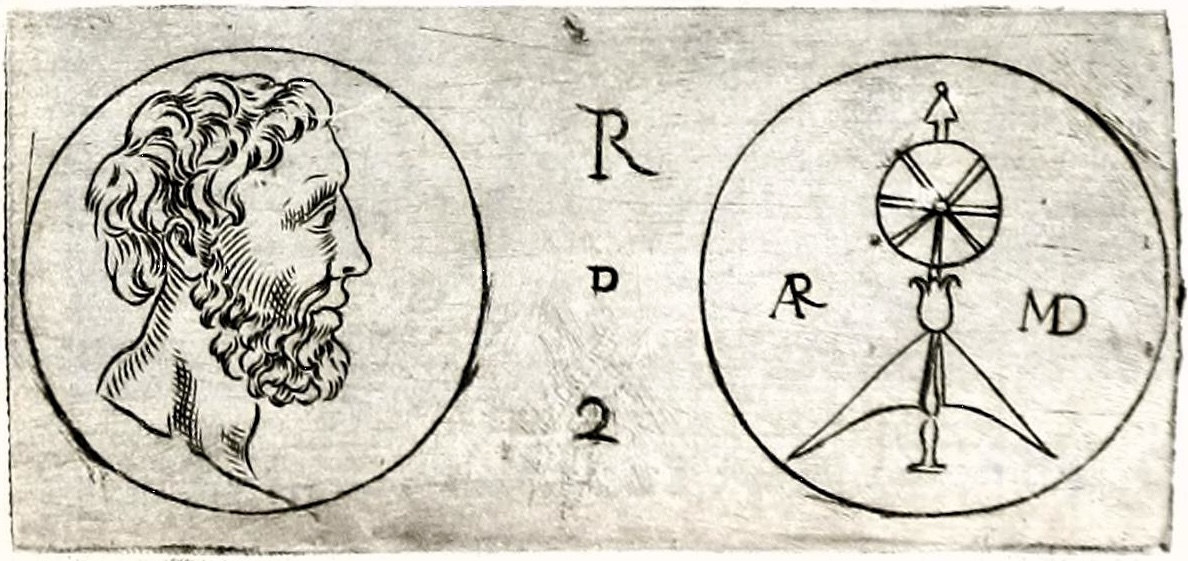
Numismatis dan arkeolog Italia Filippo Paruta (1552-1629) dan Leonardo Agostini (1593-1676) melaporkan tentang sebuah koin perunggu di Sisilia dengan potret Archimedes di bagian depan dan silinder serta bola dengan monogram ARMD dalam bahasa Latin di bagian belakang. Meskipun koin itu sekarang hilang dan tanggalnya tidak diketahui secara pasti, Ivo Schneider menggambarkan bagian belakangnya sebagai "bola yang bertumpu pada alas - mungkin gambar kasar salah satu planetarium yang dibuat oleh Archimedes," dan menyarankan bahwa itu mungkin dicetak di Roma untuk Marcellus yang "menurut laporan kuno, membawa dua bola Archimedes bersamanya ke Roma."

Ada kawah tumbukan di Bulan bernama Archimedes (29.7° N, 4.0° W) untuk menghormatinya, serta pegunungan bulan, Montes Archimedes (25.3° N, 4.6° W).

Medali Fields untuk pencapaian luar biasa dalam matematika membawa potret Archimedes, bersama dengan ukiran yang menggambarkan buktinya tentang bola dan silinder. Prasasti di sekitar kepala Archimedes adalah kutipan yang dikaitkan dengan penyair abad ke-1 Masehi Marcus Manilius, yang berbunyi dalam bahasa Latin: Transire suum pectus mundoque potiri ("Melampaui diri sendiri dan menguasai dunia").

Archimedes telah muncul di prangko yang dikeluarkan oleh Jerman Timur (1973), Yunani (1983), Italia (1983), Nikaragua (1971), San Marino (1982), dan Spanyol (1963).

Seruan Eureka! yang dikaitkan dengan Archimedes adalah moto negara bagian California. Dalam hal ini, kata tersebut mengacu pada penemuan emas di dekat Sutter's Mill pada tahun 1848 yang memicu demam emas California.